-
Linear regression머신러닝 기초 2019. 9. 22. 12:44반응형
만약 집의 면적을 알고 있을 때 집값을 예측하는 모델을 만든다고 하자. 면적과 가격의 관계를 알기 위해 아래와 같이 Regression 모델을 만들 수 있을 것이다.

f( )는 y와 x의 관계를 보여주는 함수 부분이며 epsilon은 noise를 의미한다. 아래는 몇 가지 regression model을 보여준다.
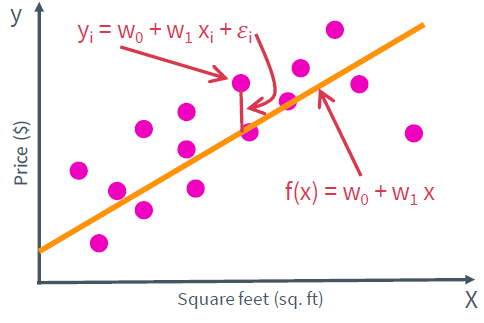
Simple linear regression model Simple linear regression model은 단순히 직선으로 표현된 모델이다. X는 input, feature를 나타내며 W0는 offset, bias를 W1는 모델의 기울기를 나타낸다. 이 W0와 W1은 parameter이며 흔히 regression coefficinet라 부른다.
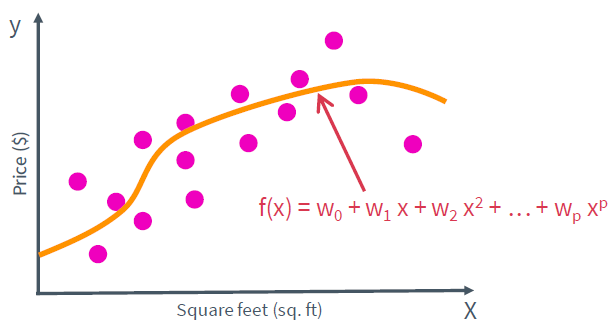
선형뿐만 아니라 더 높은 차수의 모델도 가능하다. polynomial 모델은 아래와 같다.
이러한 모델들의 일반식을 써보면 아래와 같다.
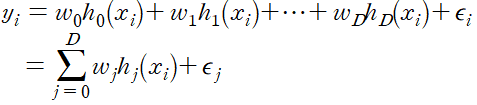
물론 집값이 오직 집의 넓이로만 결정되지는 않을 것이다. 만약 화장실의 개수 또한 집값에 영향을 미친다면, 다시 말해 모델의 input이 여러 개라면 input X는 벡터로 표현돼야 할 것이다.

일반적으로 표현하면

이고 모델은 다음과 같이 표현된다.
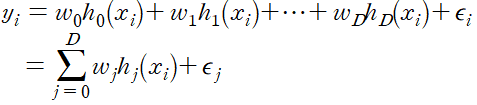
1D regression model과 형태는 동일하지만 x가 scalar가 아닌 vector라는 점에 주목해야 한다. 예를 들어 h1는 집 넓이에 대한 feture를, h2는 화장실 개수와 침대 개수의 관계에 대한 feture 등 다양한 feture를 고려할 수 있다.
이제 regression model을 실제 데이터에 적용을 해야한다. 적절한 regression model을 세우는 방법은 아래 단계를 따른다.
1. Rewrite the regression model
regression model의 일반식은 아래와 같다.
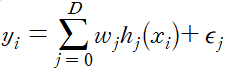
이 식을 행렬 곱으로 표현하면
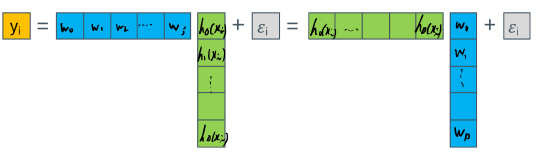
으로 표현된다. 만약 output y가 한개가 아닌 여러개인 경우에는 행렬을 확장하여 다음과 같이 표현된다.

2. Compute the cost
cost는 우리의 모델과 실제 데이터가 얼마나 차이가 나는지 나타내는 척도이다. 대표적인 cost function으로 RSS(Residual sum of squares)가 있다. input이 한개일때 RSS의 일반식은 아래와 같다.
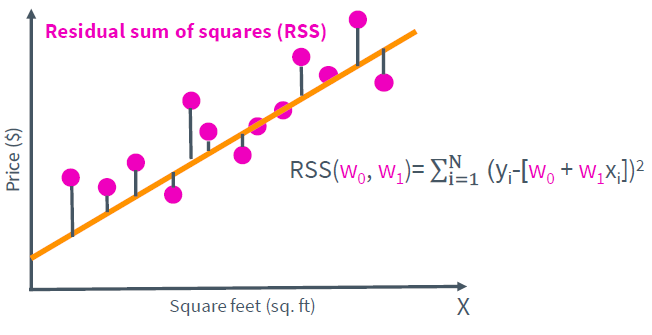
만약 input이 여러개(multiple regression)라면

이다. 간단히 표현하면 실제값 - 측정값의 제곱의 합이다. multiple regression은 위와 같이 행렬의 곱으로 표현이 가능하다.
3. Take the gradient
우리는 RSS가 감소하는 방향으로 모델을 세우고 싶으므로 RSS의 기울기 즉, gradient를 계산해야 한다. 행렬에서의 gradient의 정의는 아래와 같다.

이를 이용해 RSS의 gradient를 계산하면 아래와 같다.

이 식은 1D인 경우에도 동일하게 적용된다.
4. Set the gradient = 0
일반적으로 RSS의 최솟값은 RSS의 gradient가 0인 지점에 형성된다. 즉 이 지점이 극솟값이자 RSS가 최소가 되는 지점이다.

RSS의 gradient가 0인 지점을 찾는 방법은 크게 수학적 방식을 이용하는 closed-form과 gradient descent를 이용해 근사적으로 계산하는 방식이 있다. 우선 closed-form을 이용하는 방법은 다음과 같다.

위 방식의 가장 큰 단점은

의 역행렬을 계산해야 한다는 점인데 역행렬의 시간 복잡도는 세제곱이다. 따라서 실제 모델에서 parameter의 수가 많아지면 계산 시간은 기하급수로 증가하며 매우 오랜 시간이 걸리게 된다.
gradient descent는 마치 골짜기를 걸어 다니며 가장 낮은 위치를 찾는 과정과 비슷하다.

특정 위치에서 음의 gradient 방향을 찾아 이동하면 결국에는 최하점에 도달할 것이다.

수식으로 표현하면 다음과 같다.

즉 time step=t+1의 w는 time step t의 w에서 RSS의 gradient의 상수 배를 뺀 만큼으로 업데이트된다 이때 상수는 learning rate라 부른다. 이 식을 요소별로 접근해보면

이다. 만약 값이 underestimate 되었다면 time step=t+1 weight는 time step t의 weight보다 증가할 것이다.
gradient descent를 코드로 구현하면 다음과 같다.
def fit(self, X, y): N = len(y) self.w = np.zeros(3) # initialize w for i in range(self.iterations): # implement gradient descent prediction = np.dot(self.w, X.T) average_rss = 1/N * np.sum(np.square(y.T - prediction)) gradient = 1/N * (-2) * np.dot(y.T - prediction, X) self.w = self.w - self.lr * gradient그렇다면 왜 RSS를 최소로 만드는 것일까? 우선 노이즈 epsilon이 가우시안 분포를 따르면

을 만족한다. 따라서
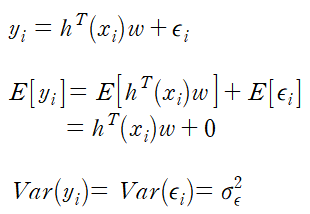
이므로

이다. 이제 MLE를 이용하기 위해 다음과 같이 표현한다.

이제 argmax를 계산하면

이므로 RSS가 최소인 지점에서 argmax를 만족하는 w이다.
반응형'머신러닝 기초' 카테고리의 다른 글
Assessing Performance (0) 2019.09.28 Numerical vs. analytic gradients (0) 2019.09.23 Maximum likelihood estimation (0) 2019.09.20 CS231n 2017 lecture 6 - part 1 (0) 2019.08.02 CS231n 2017 lecture 5 (0) 2019.07.31