Maximum likelihood estimation

예를 들어 압정을 던져 앞면과 뒷면이 나올 확률을 계산한다고 하자. 앞면, 뒷면 2가지 경우만 존재하므로 이 확률 분포는 binomial distribution을 따른다. 각각의 확률은 다음과 같다고 하자.

 

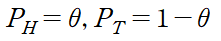
압정을 던지면 각각의 시행은 independent identically distributed(i.i.d)를 만족한다. 따라서 다음과 같이 표현할 수 있다.

 

그렇다면 앞면과 뒷면의 발생 횟수가 주어졌을 때 앞면과 뒷면이 나올 확률을 어떻게 계산할 수 있을까? 이때 필요한 것이 maximum likelihood estimation(MLE)으로 관측된 데이터의 가능성을 최대화하는 확률(theta)을 구하는 과정으로 아래와 같이 나타낸다.

 

argmax는 주어진 값을 가장 크게 만드는 theta를 반환하는 함수이다. 이때 argmax 안이 지수함수의 곱으로 이루어져 있으므로 계산의 편의를 위해 자연로그 ln을 취해준다. ln은 단조 증가함수 이므로 계산 결과에 영향이 없다. 위 식을 정리하면 아래와 같다.

 

argmax 안을 최대로 만드는 theta를 찾기 위해 theta에 대해 미분하면

 

이므로 theta를 계산할 수 있으며 충분히 예상 가능한 결과이기도 하다.

MLE의 장점은 매우 직관적이라는 점이다. 그리고 별다른 가정을 하지 않고 주어진 관측 결과를 바탕으로 쉽게 계산할 수 있다. 물론, 관측 결과가 이항 분포를 따를 것이라는 가정이 들어갔지만 다른 추정법에 비해서는 가정이 약한 편이다.

MLE는 빈도론을 기반으로 한다. 관측결과에 의존해서 판단하기 때문에 관측 결과의 크기(관측 횟수)와 질(관측 결과의 정확성)에 따라서 theta 추정의 성패가 크게 좌우된다.

 

그렇다면 관측결과의 크기와 theta의 값의 정확도는 어떤 관계일까? 전체 관측 횟수를 N이라 하면

 

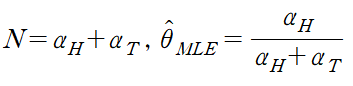
이고 실제 정확한 값인 theta*에 대해 다음 조건을 만족한다. (Hoeffding’s Inequality)

 

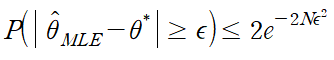
위 식은 모든 양수 epsilon에 대해 만족하므로 N이 증가할수록 error가 감소한다. 즉 N이 클수록 theta는 정확해지며 이렇게 theta를 찾아내는 과정을 Probably Approximate Correct(PAC) learning이라 부른다.

 

지금까지 MLE에서는 2가지 경우만 존재하는 binomial distribution 데이터만 증명했지만 실제로는 continuous-valued인 데이터가 대부분이다. 이런 continuous-valued 데이터들은 (ex 키, 몸무게) 대부분 Gaussian을 따른다. 1차원 Gaussian probability density function은 아래와 같다.

 

Gaussain의 유명한 두 가지 성질은 다음과 같다.

 

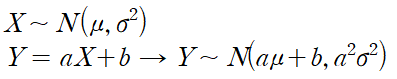
Affine transformation

Sum of Gaussians

이제 MLE를 이용해 Gaussian의 mean과 variance를 계산해보자. binomial distribution과 마찬가지로 각각의 데이터들은 모두 i.i.d를 만족한다고 가정한다. 우선 전체 데이터의 집합 중 N개의 집합(sample data)을 고른 D를 아래와 같이 정의하자.

 

그렇다면 likelihood function은 다음과 같이 표현된다.

 

각 확률은 independent 이므로

 

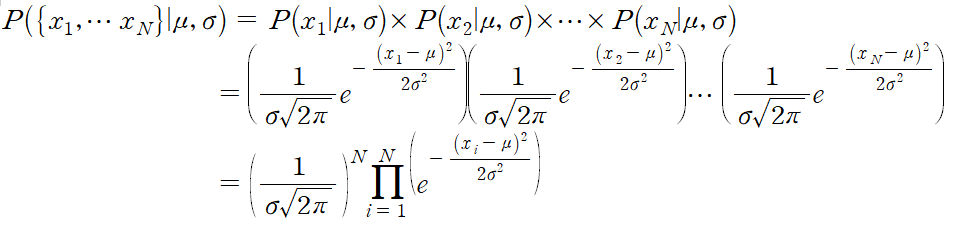
이다. 이제 계산의 편의를 위해 자연로그를 취하면

 

이다. 주어진 MLE의 parameter가 mean과 variance 두 가지 이므로 각각에 대해 미분을 해야 한다. 우선 mean에 대해 미분하면

 

이며 이 값은 sample mean과 동일하다. 다음으로 variance에 대해 미분하면

 

이다. 하지만 실제로 이 값은 분산에 대해 biased estimates(분산의 편파 추정치)인데 실제로 모집합을 추정하기 위해 계산된 variance의 기댓값은 모집단의 variance와 같은 값이 아니라 보다 작은 값을 추정하게 된다. unbiased estimates(분산의 불편파 추정치)를 계산하기 위해서는 위의 공식이 아래와 같이 수정되어야 한다.

 

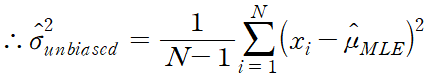
분모의 N이 N-1이 된 점을 주목하면 된다. 실제로 MLE로 계산한 variance가 biased인 이유를 증명하면 아래와 같다.

 

이고

 

임을 이용하면

 

이므로 biased 되어있다.