CS231n 2017 lecture 4 - part 2

 

만약 한 노드의 출력단이 그림과 같이 2개 이상으로 분리되어있는 경우 gradient는 각 출력 노드에서 계산한 gradient의 합으로 계산된다.

 

 

실제로 $x, y, z$의 값은 실수가 아닌 벡터인 경우가 대부분일 것이므로 이때 gradient는 Jacobian matrix(자코비안 행렬, 다변수 벡터 함수의 도함수 행렬이다.)로 표현될 것이다. Jacobian matrix는 아래와 같이 정의된다.

 

 

 

4. Vectorized operations

 

 

이제 backpropagation을 행렬에 적용해본다. 위의 그림에서 $\frac{\partial L}{\partial x}=\frac{\partial f}{\partial x}\frac{\partial L}{\partial f}$ 이므로 local gradient $\frac{\partial f}{\partial x}$는 Jacobian matrix이고 그 크기는 4096X4096이 될 것이다. 또한 노드의 계산식이 $f(x)=\max(0,x)$ 이므로  Jacobian matrix의 원소들은 대각선을 제외한 모든 성분이 0이고 대각선은 0 또는 1의 값을 가지는 행렬이 될 것이다.

 

이제 아래와 같은 computational graphs에서 gradient를 계산해보자.

 

 

우선 L2 Regularization이 적용된 $f$에서 $\frac{\partial f}{\partial q_i}=2q_i$ 이므로 $f$의 $q$에 대한 gradient는 위와 같이 된다. 

 

 

$q=W\cdot{x}$ 이므로 같은 방법으로 계산하면 $W$에 대한 $f$의 gradient는 $2q\cdot{x^T}$이다. $x$의 전치 행렬을 곱해야 올바른 행렬 모양이 나온다.

 

 

5. Neural Networks

 

 

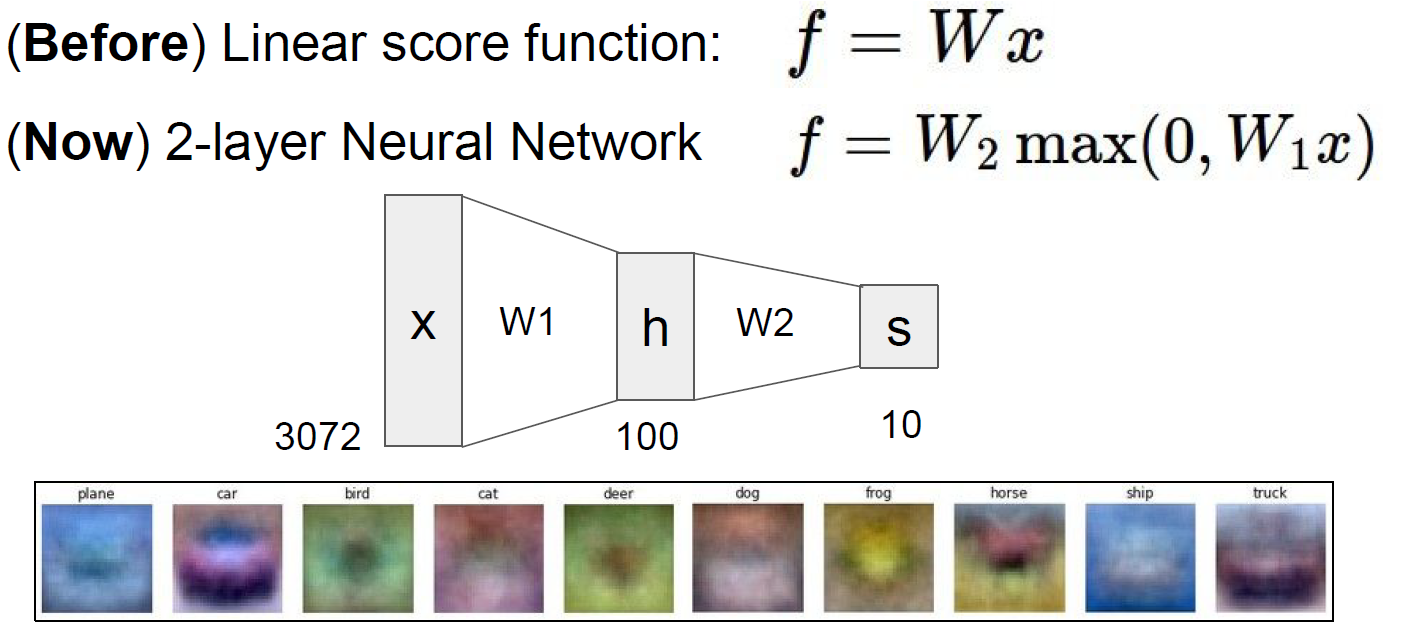
지금까지 $f=Wx$의 Linear score function에 다뤘지만 Layer를 한층 더 늘려 2-layer Neural Network를 생각해볼 수 있다. 2-layer Neural Network의 예로 $f=W_2\max(0, W_1x)$를 생각해보자 ($\max(0, W_1x)$는 뒤에서 언급할 ReLu function이다.) 위의 그림에서 100x1 행렬의 원소는 최종 10개의 class를 분류할 템플릿 역할을 한다. 기존의 Linear score function에서는 이 템플릿이 10개에 그쳤지만 이 2-layer Neural Network에서는 100개로 증가한다.

 

 

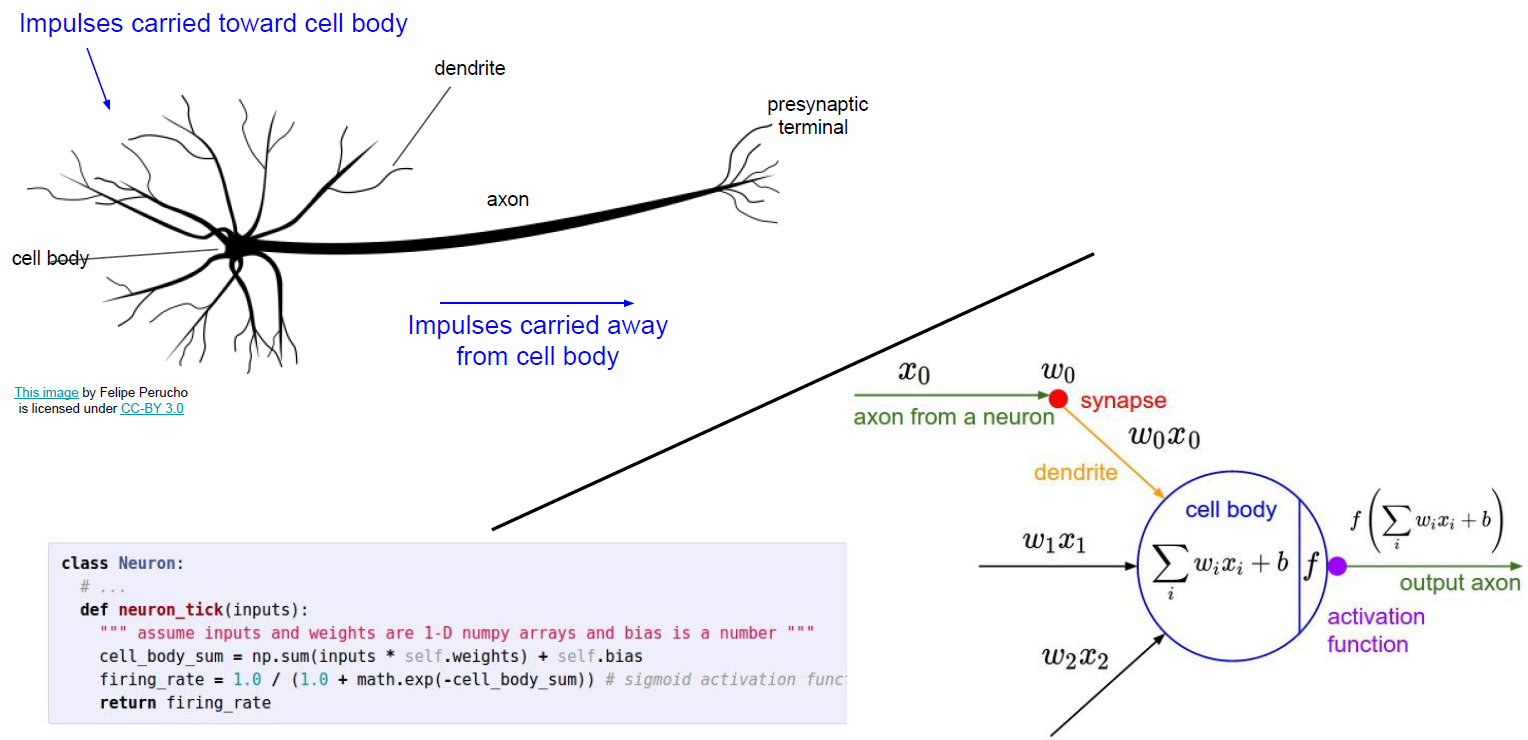
신경 세포와 Neural Network는 비슷한 점이 많다. 물론 신경세포가 훨씬 복잡하지만 한 노드에서 다른 노드로 이동할때 Neural Network는 Activation function를 거친다. Activation function의 종류는 다양하지만 주로 아래의 Activation function를 사용한다.