-
CS231n 2017 lecture 3머신러닝 기초 2019. 7. 26. 15:04반응형
1. Linear Classifier
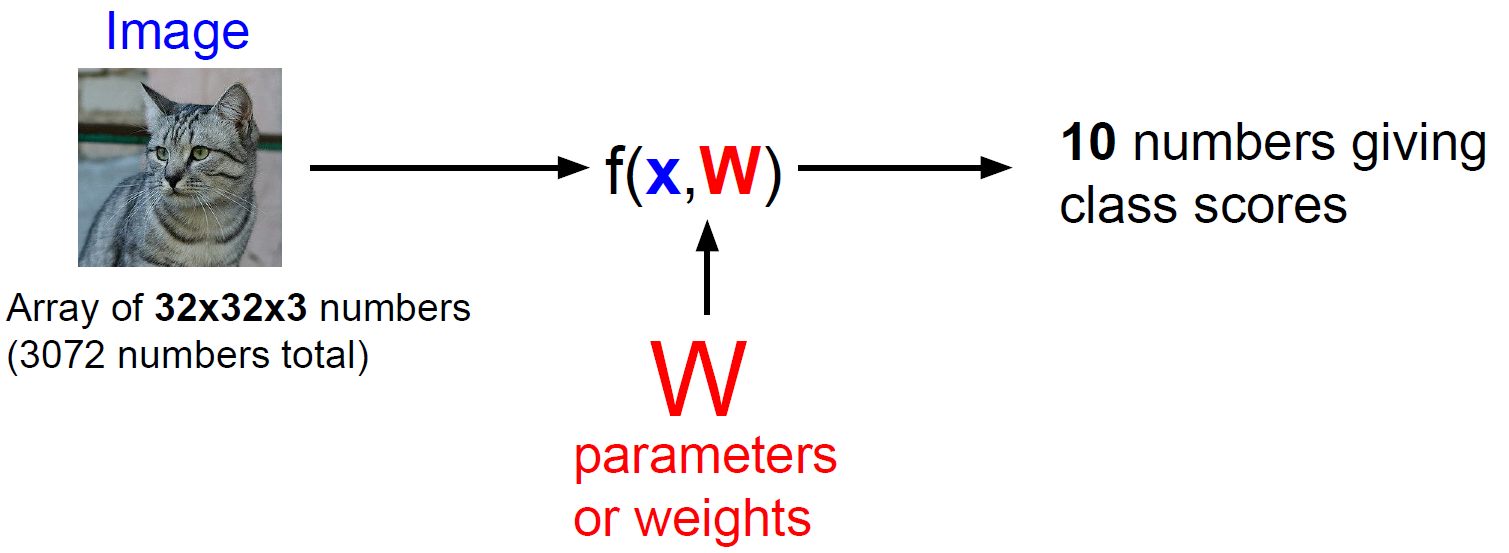
Linear Classifier는 Parametric model의 가장 단순한 형태이다. Parametric model에서 일반적으로 입력 이미지를 x, parameters, 즉 weights(가중치)를 W라 표현한다. Parametric model에서 $f(x, W)$를 수행하면 이미지 카테고리에 대한 각각의 점수가 나온다. CIFAR-10이라면 10개의 점수가 나오는 것이다.
$f(x, W)$의 가장 쉬운 형태는 $f(x, W)=Wx$로 단순 두 항을 곱하는 것이다. (이것이 Linear Classifier의 기본이다.) 물론 $x, W$ 모두 벡터이기 때문에 각각의 차원을 나타내면 아래와 같다.

입력 이미지가 32x32x3이기 때문에 하나의 긴 열(column) 벡터로 표현하면 3072x1이 된다. 출력은 10x1의 10개의 카테고리의 점수 벡터가 출력되어야 하므로 가중치는 10x3072가 되어야만 한다.
b는 Bias(바이어스)라 불리는 항인데 특정 class에 우선권을 부여하는 역할을 한다. 예를 들어 데이터 셋에 강아지가 고양이에 비해 훨씬 적다면 고양이에 대한 바이어스 항이 커지게 된다. 그림으로 표현하면 아래와 같다.

만약 임의의 가중치 W로 3개의 이미지(고양이, 자동차, 개구리)의 점수를 예측한 결과가 아래와 같다고 하자 예를 들어 자동차의 경우는 자동차에 가장 높은 점수를 주었으므로 올바른 가중치이지만 고양이와 개구리는 그렇지 못하다.
이 가중치가 얼마나 정확한지 정량화할 방법이 필요한데 이때 loss function(손실함수)를 이용할 수 있다.

2. Loss function - Multiclass SVM loss
loss function은 일반적으로 $L_i$로 표현되는데 $i$번째 클래스 입력 이미지를 $x_i$, 정답 클래스를 $y_i$, 가중치를 $W$라고 하면 loss $L$은 아래와 같이 표현된다.
$$L=\frac{1}{N}\sum_i^{}L_i(f(x_i, W), y_i)$$
즉 전체 loss는 각 클래스의 loss의 평균값과 같다.
이러한 loss function은 여러가지 방법으로 계산될 수 있는데 여기서는 Multiclass SVM(support vector machine) loss를 다룬다. Multiclass SVM loss의 loss function은 아래와 같이 정의된다.
$$L_i=\sum_{j\neq{y_i}}^{}\max(0, s_j-s_{y_i}+1)$$
이때 $s_j$는 j번째 클래스의 점수, $s_{y_i}$는 정답 클래스의 점수를 의미한다. 이를 그래프로 표현하면 아래와 같은데 그 모양이 Hinge(경첩)과 비슷해 Hinge loss라고도 부른다.
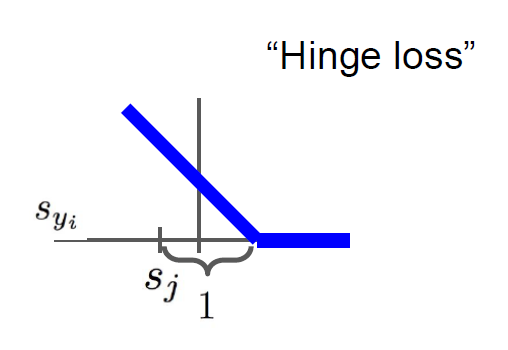
$\max(0, s_j-s_{y_i}+1)$에서 +1은 Safety margin이라 불리는 항인데 크게 중요하지는 않다. 이 값이 변하면 전체 loss가 rescale 될 뿐이다. Multiclass SVM loss를 각각의 클래스에 계산한 결과는 아래와 같다.

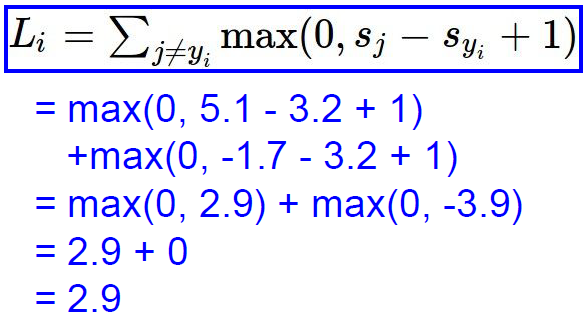


Multiclass SVM loss는 아래와 같이 파이썬 코드로도 표현 가능하다.

Multiclass SVM loss에서 loss는 최소 0이 가능하다. 그렇다면 loss가 0이되는 W는 하나만 존재할까? 사실 그렇지 않다. 가장 간단한 예로 W의 loss가 0이 됐다면 2W, 3W 모두 loss가 0이기 때문이다.
Linear Classifier를 이용해 학습하면 가장 큰 문제는 트레이닝 셋에 overfit 될수 있다는 점이다. 예를 들어 아래 그림의 파란색 점이 트레이닝 셋이고 초록색이 테스트 셋이라 하면 overfit에 의해 파란색 곡선처럼 트레이닝 셋이 과하게 적합한 모델을 찾을 것이다. 따라서 새로운 초록색 데이터와 잘 맞지 않는 문제가 생긴다. 사실 이 예에서 가장 이상적인 모델은 초록색 직선과 같은 단순한 모델이다. 실제 Linear Classifier에서는 Regularization(정규화)를 통해 이 문제를 해결한다.

위의 loss function 수식에 Regularization항을 추가하면 아래와 같이 된다.
$$L=\frac{1}{N}\sum_i^{}L_i(f(x_i, W), y_i)+\lambda{R(W)}$$
Regularization 항은 모델이 좀더 단순한 W를 선택하도록 해준다. 이때 $ \lambda$는 hyperparameter이다. Regularization 항이 어떻게 overfit을 막는지에 대한 내용은 뒤에서 다룬다.

위와 같이 Regularization은 다양한 방법으로 계산될 수 있다. 가장 대표적으로 L2 Regularization을 사용하는데 L2 Regularization은 가중치 행렬 W에 대한 Euclidean norm(노음은 벡터공간의 벡터들에 대해 일종의 ‘길이’ 혹은 ‘크기’를 부여하는 함수이다.)이다. 예를들어 L2 norm은 아래와 같이 계산된다.
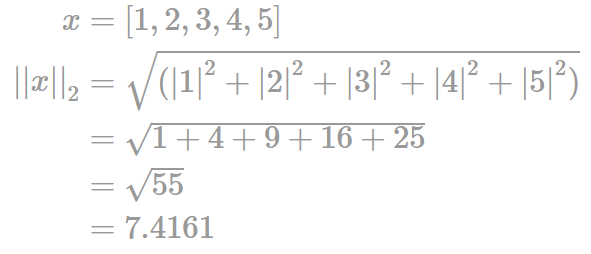
만약 $x, w1, w2$가 아래와 같이 주어졌다면 L2 Regularization은 L2 norm이 더 작은 $w2$를 선호할 것이다(더 작은 loss를 가지가 때문, L1 Regularization 값은 두 가중치가 같다.).

즉 다시말해 L2 Regularization은 $x$의 특정 요소에만 의존하기 보다는 모든 픽셀이 골고루 영향을 미치기를 원할때 사용하면 좋다.
3. Loss function - Softmax
Multiclass SVM loss에서는 각 클래스의 점수 자체에는 크게 의미를 두지 않았다. 즉 점수의 높낮이만 알 수 있었는데, Multinomial Logistic Regression 이하 Softmax는 점수 차제에 의미를 둔다. Softmax는 각각 클래스 점수에 따른 실제 그 클래스가 맞을 확률을 이용한다. 수식으로 표현하면 아래와 같다.
$$P(Y=k|X=x_i)=\frac{e^{s_k}}{\sum_j^{}e^{s_j}}$$
이 함수를 softmax function이라 하며 확률이기 때문에 0과 1사이의 값을 가진다. 이제 loss function은 0부터 무한대의 값을 가지므로 단조 증가함수인 $\log$를 이용하면 아래와 같이 표시된다.
$$L_i=-\log_{}{P(Y=k|X=x_i)} $$
실제로 계산하보면 아래와 같다.

Multiclass SVM loss와 Softmax를 비교해보면 다음과 같다.
 반응형
반응형'머신러닝 기초' 카테고리의 다른 글
CS231n 2017 lecture 5 (0) 2019.07.31 CS231n 2017 lecture 4 - part 2 (0) 2019.07.30 CS231n 2017 lecture 4 - part 1 (0) 2019.07.28 CS231n 2017 lecture 2 (0) 2019.07.21 CS231n 2017 lecture 1 (0) 2019.07.20