-
CS231n 2017 lecture 2머신러닝 기초 2019. 7. 21. 11:56반응형
https://www.youtube.com/watch?v=OoUX-nOEjG0&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=3&t=0s
1. Image Classification

Image의 Object가 무엇인지 인간은 매우 쉽게 알 수 있지만 컴퓨터는 그렇지 못하다. 같은 고양이 사진도 우리는 왼쪽과 같이 이해하지만 컴퓨터는 800 X 600 X 3의 matrix로 이해한다. (x3은 이미지의 RGB 3개의 채널을 의미한다.) Image Classification이 어려운 이유는 크게 아래와 같은 이유가 존재한다.
-
Viewpoint variation(시점 변화) : 객체의 단일 인스턴스는 카메라에 의해 시점이 달라질 수 있다.
-
Scale variation(크기 변화) : 비주얼 클래스는 대부분 그것들의 크기의 변화를 나타낸다(이미지의 크기뿐만 아니라 실제 세계에서의 크기까지 포함함).
-
Deformation(변형) : 많은 객체들은 고정된 형태가 없고, 극단적인 형태로 변형될 수 있다.
-
Occlusion(폐색) : 객체들은 전체가 보이지 않을 수 있다. 때로는 물체의 매우 적은 부분만이 보인다.
-
Illumination(조명) : 조명의 영향으로 픽셀 값이 변형된다.
-
Background clutter(배경 분규) : 객체가 주변 환경에 섞여 알아보기 힘들게 된다.
-
Intraclass variation(내부 클래스의 다양성) : 분류해야 할 클래스는 범위가 큰 것들이 많다. 예를 들어 의자의 경우, 매우 다양한 형태의 객체가 있다.
2. Data-driven approach(데이터 기반 방법론)

일반적인 방법으로 Image Classification 알고리즘을 작성하는 것은 매우 어렵다. 그러므로, 코드를 통해 직접적으로 모든 것을 카테고리로 분류하기보다는 좀 더 쉬운 방법을 사용해야 한다. 먼저 컴퓨터에게 각 클래스에 대해 많은 예제를 주고 나서 이 예제들을 보고 시각적으로 학습할 수 있는 학습 알고리즘을 개발하는 것이다. 이런 방법을 data-driven approach이라고 한다. 이 방법은 라벨화가 된 이미지들 training dataset이 처음 학습을 위해 필요하다. 위의 그림은 이런 데이터셋의 예이다.
3. Nearest Neighbor Classifier
Image Classification을 위한 Classifier(분류기)를 제작하는 가장 쉬운 방법은 Nearest Neighbor를 이용하는 것이다. 이 방법은 부정확하며 이미지 분류에는 거의 사용하지 않지만 이미지 분류 문제에 대한 기본적인 접근 방법을 알 수 있다. 가장 간단하면서 유명한 Image Classification dataset은 CIFAR-10이다.
http://www.cs.toronto.edu/~kriz/cifar.html
CIFAR-10 and CIFAR-100 datasets
< Back to Alex Krizhevsky's home page The CIFAR-10 and CIFAR-100 are labeled subsets of the 80 million tiny images dataset. They were collected by Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton. The CIFAR-10 dataset The CIFAR-10 dataset consists of 60000
www.cs.toronto.edu
이 데이터셋은 60,000개의 작은 이미지로 구성되어 있고, 각 이미지는 32x32 픽셀 크기이다. 각 이미지는 10개의 클래스중 하나로 라벨링 되어 있다. 이 60,000개의 이미지 중에 50,000개는 학습 데이터셋 (training dataset), 10,000개는 테스트 셋으로 분류된다.

CIFAR-10 dataset 이미지를 비교하는 가장 간단한 방법 중 하나는 이미지를 각각의 픽셀 값으로 비교하고, 그 차이를 모두 더하는 것이다. 이를 L1 distance(L1 거리)를 계산한다고 하는데, 비교할 2개의 이미지의 벡터를 각각 $I _{1}, I _{2}$라고 하면 다음과 같은 방법으로 계산된다.
$$d_1(I_1, I_2)=\sum_p^{}|I_1^p-I_2^p|$$
이를 그림으로 표현하면 아래와 같다.
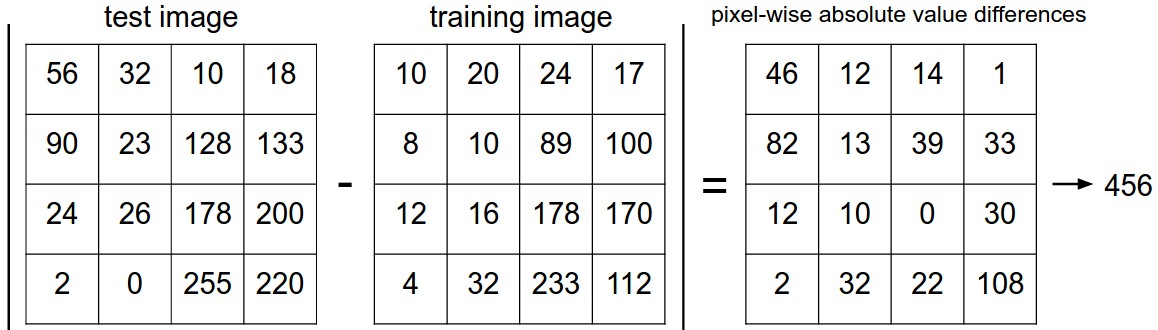
만약 두 이미지가 똑같을 경우에는 결과가 0일 것이고, 두 이미지가 매우 다르다면 결과값이 클 것이다. 이 Nearest Neighbor Classifier를 구현한 코드는 아래와 같다.

이 코드를 실행해보면 이 분류기는 CIFAR-10에 대해 정확도가 38.6% 밖에 되지 않는다는 것을 확인할 수 있다. 또한 이 코드의 시간 복잡도는 Train단계에서 $O(1)$, Predict 단계에서 $O(N)$이므로 오히려 Predict 단계에서 더 느리다. 실제 이러한 Nearest Neighbor Classifier를 스마트폰 등에서 쉽게 사용하기 위해서는 Predict 단계의 속도가 더 빨라야 하므로 좋지 않은 방법이다.
벡터 간의 거리를 계산하는 방법은 L1 거리 외에도 매우 많다. 또 다른 일반적인 방법으로, 기하학적으로 두 벡터 간의 유클리디안 거리를 계산하는 것으로 해석할 수 있는 L2 distance(L2 거리)가 있다. 이 거리의 계산 방식은 다음과 같다.
$$d_1(I_1, I_2)=\sqrt{\sum_p^{}(I_1^p-I_2^p)^2}$$
일반적으로, L2 거리는 L1 거리에 비해 두 벡터 간의 차가 커지는 것에 대해 훨씬 더 크게 반응한다. 즉, L2 거리는 하나의 큰 차이가 있는 것보다 여러 개의 적당한 차이가 생기는 것을 선호한다.
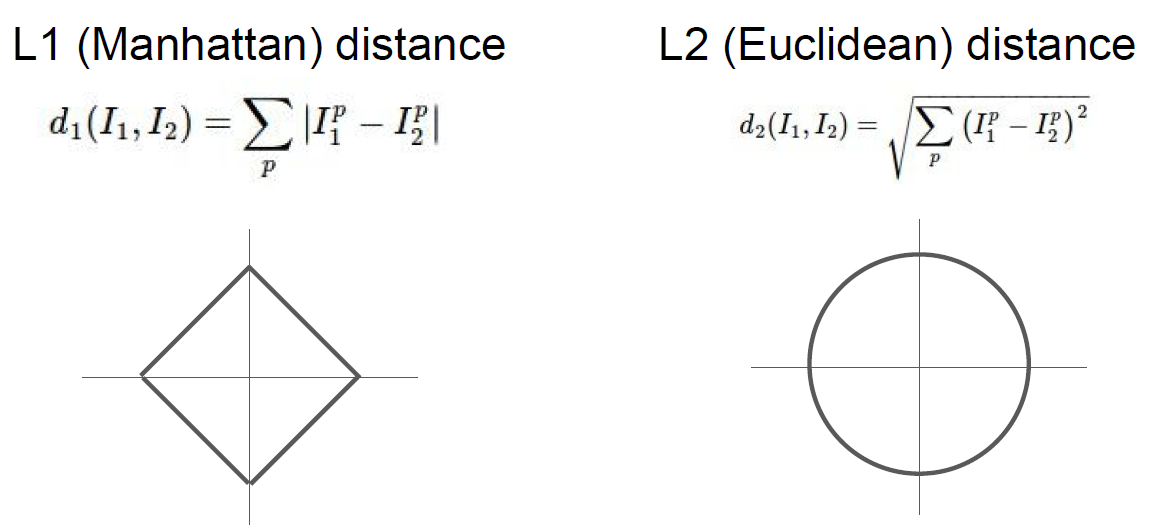
L1 distance vs L2 distance 4. K-Nearest Neighbors
K-Nearest Neighbors는 학습 데이터셋에서 가장 가까운 하나의 이미지만을 찾는 것이 아니라, 가장 가까운 k 개의 이미지를 찾아서 테스트 이미지의 라벨에 대해 투표하도록 하는 것이다. 일반적으로 k 값이 커질수록 분류기는 이상점(outlier)에 더 강인하고, 분류 경계가 부드러워지는 효과가 있다.

실제 동작 모습은 http://vision.stanford.edu/teaching/cs231n-demos/knn/ 에서 확인 가능하다.
5. Hyperparameters
그렇다면 최적의 Classifier 성능을 가지는 k값과 Distance ($L_1, L_2$)를 결정해야 하는데, 이러한 선택들을 hyperparameters라 부른다. 이때 중요한 점은 최적의 Classifier 성능을 구할 때 hyperparameter 값을 조정하기 위해 테스트 셋을 사용하면 절대 안 된다는 것이다. 실제로 알고리즘을 평가할 때인 맨 마지막 단 한 번을 제외하고는 절대 쳐다봐서는 안 된다. 그렇게 하지 않는다면, 모델의 hyperparameter들이 테스트 셋에서는 잘 동작하도록 튜닝이 되어 있지만, 실전에서 모델을 사용할 때 상당히 성능이 낮아지는 것을 확인할 수 있다. 흔히 이러한 현상을 테스트 셋에서 overfit 되었다고 말한다.
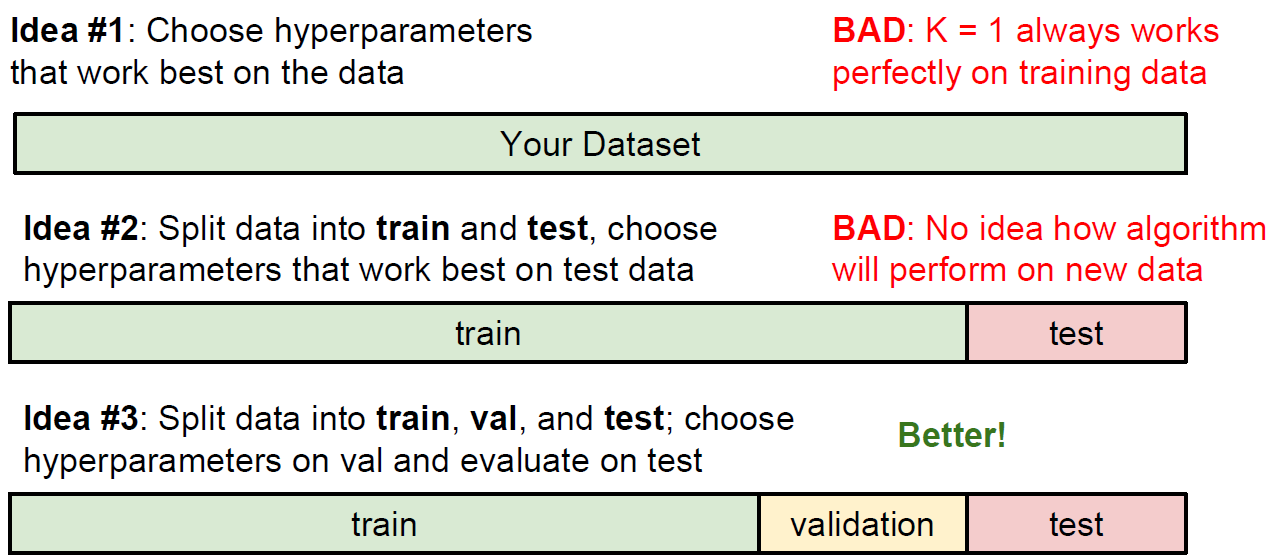
다행히 이른바 validation set(검증 셋)으로 불리는, 약간 적은 수의 트레이닝 셋과 나머지로 나누면 이러한 문제를 해결할 수 있다. 이 검증 셋은 hyperparameter 들을 튜닝할 때, 가짜 테스트 셋으로 활용된다.
만약 학습 데이터 셋의 크기가 작을 경우, 조금 더 정교한 방식으로 cross-validation(교차 검증)이라는 hyperparameter 튜닝 방법을 사용한다. 예를 들어, 5-fold 교차 검증에서는 학습 데이터를 5개의 동일한 크기의 그룹(fold)으로 쪼갠 뒤, 4개를 학습용으로, 1개를 검증용으로 사용한다. 그다음에는 어떤 그룹을 검증 셋으로 사용할지에 따라 iteration(반복)을 돌고, 성능을 평가하고, 각 그룹에 대해 평가한 성능을 평균을 낸다.
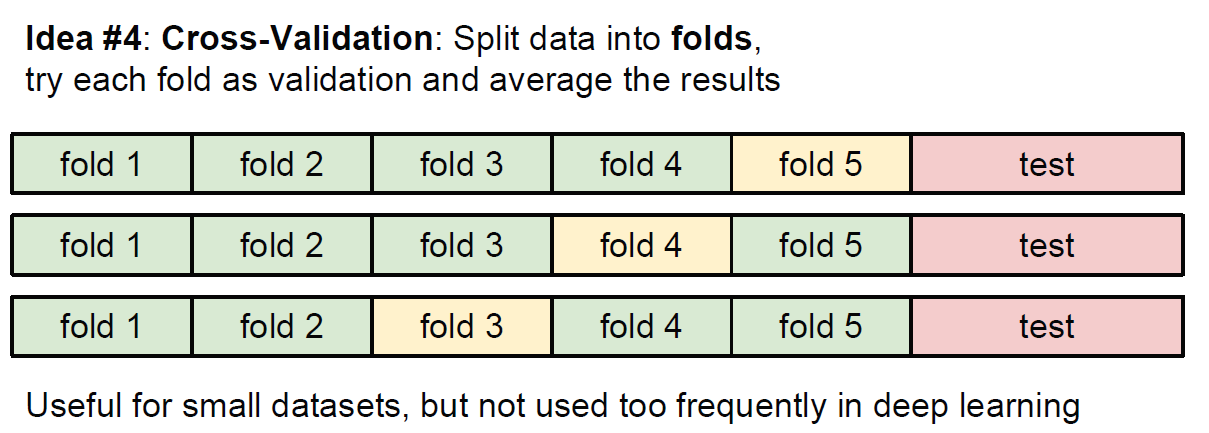
아래는 5 folds Cross-Validation의 결과이다. 그래프에서 선은 각 kk에서의 결과의 평균으로 그려져 있고, 에러 바는 표준 편차를 나타낸다. 이 경우 k=7에서 가장 높은 정확도를 보인다.

6. Nearest Neighbor Classifier의 단점
- 앞에서 언급했듯 Predict 단계(테스트 단계)의 속도가 느리다.
- 고차원 데이터(이미지)에서의 픽셀 값 기준 거리는 매우 비 직관적인 경우가 많다. 예를 들어 아래 4개의 이미지의 픽셀 값은 L2 거리를 기준으로 모두 같은 거리만큼 떨어져 있다.

-
Curse of dimensionality(차원의 저주) 문제가 발생한다. 차원의 수가 증가할수록 Nearest Neighbor Classifier에 필요한 데이터가 기하급수적으로 증가한다.
 반응형
반응형'머신러닝 기초' 카테고리의 다른 글
CS231n 2017 lecture 5 (0) 2019.07.31 CS231n 2017 lecture 4 - part 2 (0) 2019.07.30 CS231n 2017 lecture 4 - part 1 (0) 2019.07.28 CS231n 2017 lecture 3 (0) 2019.07.26 CS231n 2017 lecture 1 (0) 2019.07.20 -