CS231n 2017 lecture 4 - part 1

1. Optimization

 

Optimization(최적화)는 최저의 loss를 가지는 가중치 $W$를 찾는 과정이다. 이 과정은 마치 넓은 골짜기를 걸어 다니며 고도가 제일 낮은 곳을 찾는 과정과 비슷하다.

 

 

물론 임의의 $W$를 계속 업데이트해 optimization을 할 수도 있지만 이 방법은 극단적으로 오래 걸린다. 그래서 사용하는 방법은 slope(경사)를 이용하는 것인데 loss가 감소하는 방향으로 $W$를 변화시키다 보면 결국에는 최적의 $W$를 찾을 수 있을 것이다.

 

일차원 벡터에서의 경사는 아래와 같이 표현된다.

$$\frac{df(x)}{dx}=\lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}$$

만약 고차원의 벡터라면 gradient를 이용해야 된다. gradient는 아래와 같이 정의된다.

$$\triangledown{f}=\left({\frac{\partial f}{\partial x_1}+\frac{\partial f}{\partial x_2}+\cdot\cdot\cdot+\frac{\partial f}{\partial x_n}}\right)$$

gradient는 아래와 같이 $W$의 원소를 아주 조금씩 변화시키면서 계산할 수 있다. 하지만 이러한 방법은 매우 비효율적이라 사용하지 않는다. 참고로 이런 방식의 계산법을 numerical gradient 라고 한다.

 

 

이보다 더 쉬운 방법은 미분의 계산 공식을 이용하는 것이다. 이러한 방법을 analytic gradient 이라고 하는데 analytic gradient는 입력 값을 조작할 필요가 없이, 수학(미분)으로 공식을 유도할 수 있다. 물론 실제로는 analytic gradient를 이용해 기울기를 계산한 뒤 numerical gradient로 다시 한번 확인하는 과정을 거친다.

 

 

2. Gradient Descent

 

Loss function의 gradient를 계산할 수 있으므로 gradient를 반복적으로 평가 한 다음 매개 변수 업데이트하는 절차를 Gradient Descent 이라고 한다. 아래 코드를 보면 step_size라는 항이 있는데 이 값을 조절하여 learnig rate를 조절할 수 있다. 이 값을 적절히 구하는 것이 학습의 성능을 결정하는 중요한 역할을 한다.

 

 

 

학습의 속도를 빠르게 하기 위해 mini-batch(미니배치)를 사용하기도 한다. 매 gradient descent 과정에서 모든 학습 데이터를 사용하는 것이 아닌 32개, 64개, 128개 등등 2의 거듭제곱의 수를 가진 데이터 셋을 임의의 로 추출하는 것이다.  2의 제곱수를 이용하는 이유는 많은 벡터 계산이 2의 제곱수가 입력될 때 더 빠르기 때문이다.

 

 

3. Backpropagation

 

Computational graphs는 일련의 연산 과정을 그래프로 나타낸 것이다. 앞선 강의에서 표현한 loss function $L=\frac{1}{N}\sum_i^{}L_i(f(x_i, W), y_i)+\lambda{R(W)}$을 computational graphs로 표현하면 아래와 같다.

 

 

computational graphs는 backpropagation(역전파)를 설명할때 유용하게 사용된다. 우선 아래와 같은 간단한 형태의 computational graphs가 존재한다고 하자.

 

 

computational graphs는 $f(x, y, z)=(x+y)z$를 의미하며 각각의 초기값은 초록색 숫자로 표시되어있다. 이제 각각의 gradient를 계산해보자. 계산을 위해 중간의 +노드의 매개변수를 $q$라고 하자. 우선 아래의 식들을 사용할 수 있을 것이다.

 

 

우리는 입력값 (여기서는 $x, y, z$)의 변화에 따른 출력값 (여기서는 $f$)의 변화, optimization 관점으로는 $W$의 변화에 따른 loss의 변화, 즉 gradient($\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}$)를 계산해야 된다. 이 값들은 바로 계산되기 어려워 Backward Pass로 계산되어야 한다. 즉 $\frac{\partial f}{\partial f}=1$, $\frac{\partial f}{\partial z}=q=3$, $\frac{\partial f}{\partial q}=z=-4$ 순으로 계산한다. $\frac{\partial f}{\partial x}$의 경우 Chain rule를 이용해 쉽게 계산할 수 있다.

$$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}=-4\times1=-4$$

같은 방법으로 $\frac{\partial f}{\partial y}$까지 계산하면 결과는 아래와 같다.

 

 

이 backpropagation의 계산방법을 좀더 일반화 하여 생각해보면 다음과 같다. 아래와 같은 노드에서 Forward Pass로 local gradient($\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}$)를 계산한다. 코드로 구현할 때는 이 값을 메모리에 저장해두면 된다.

 

 

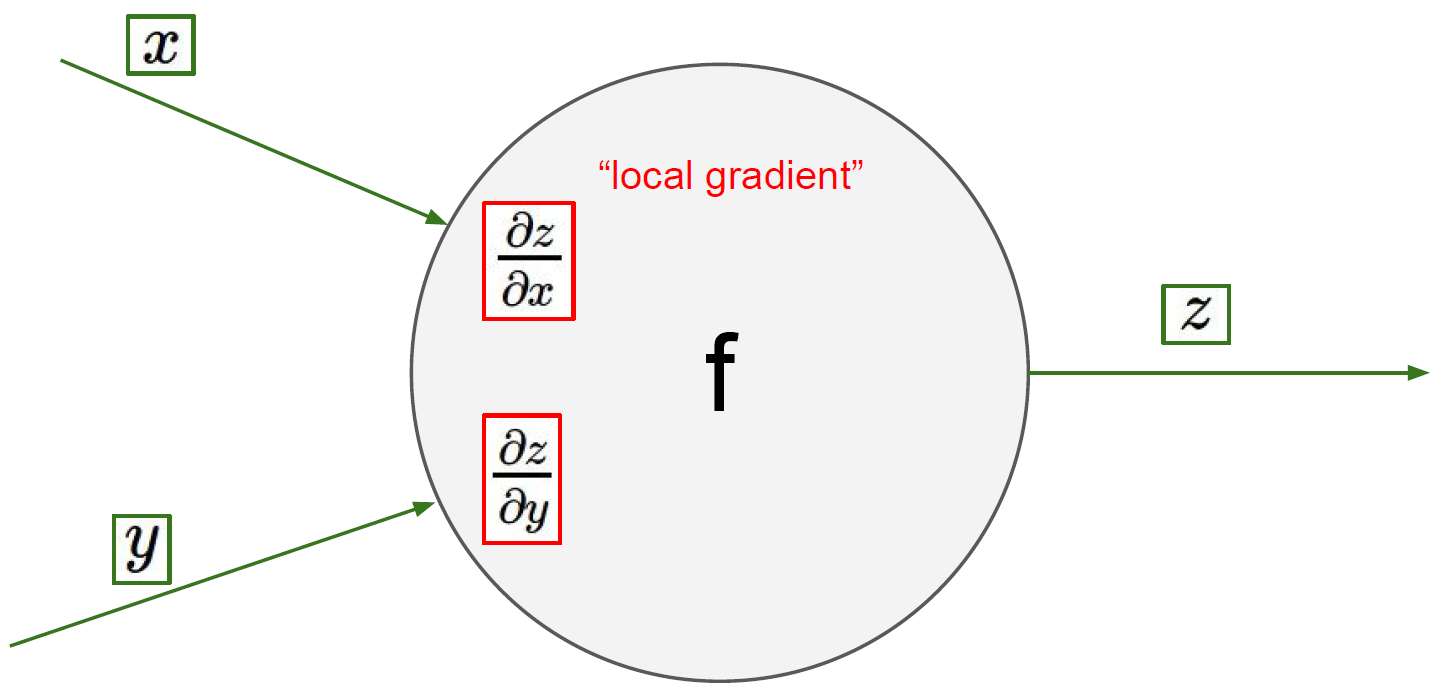
그 다음 Backward Pass로 계산하여 global gradient($\frac{\partial L}{\partial z}$)를 계산한다.

 

'

마지막으로 global gradient와 local gradient를 곱해(chain rule에 의해) backpropagation을 완성한다. 이 과정을 계속 반복하면 된다.

 

 

다른 예시로 아래와 같은 computational graphs에 적용할 수 있다.

 

 

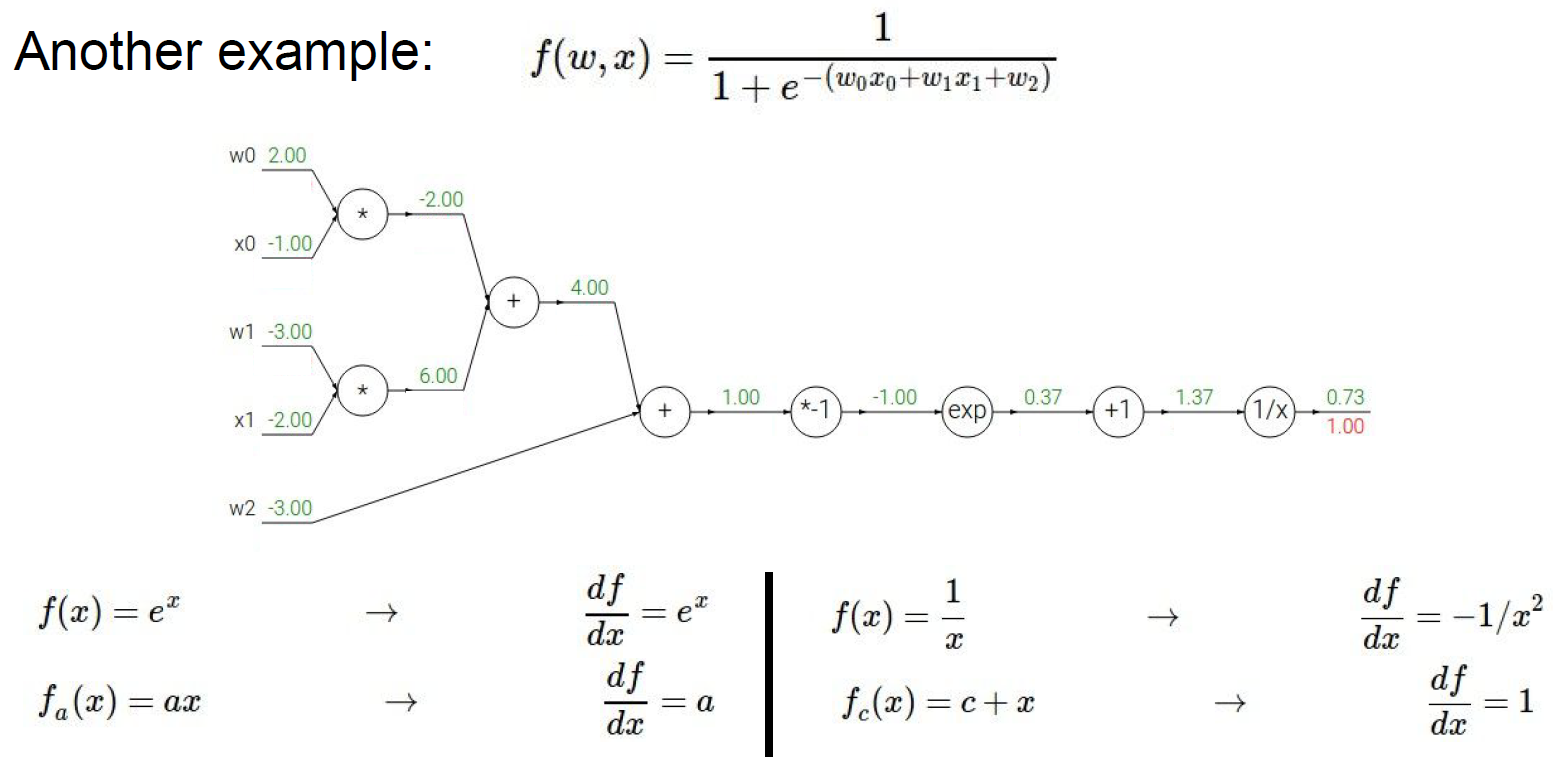
같은 방법으로 gradient를 계산하면 아래와 같다.

 

 

특이하게 파란색 상자의 부분을 수식으로 표현하면 다음과 같다.

$$\sigma(x)=\frac{1}{1+e^{-x}}$$

이 함수를 시그모이드 함수(sigmoid function)라고 한다. 시그모이드 함수는 특별한 성질이 있는데 gradient를 계산하면 아래와 같이 단순화 된다.

 

따라서 파란색 상자를 하나의 시그모이드 노드로 생각하고 gradient를 구해보면 정확히 동일한 값이 나온다. 그러므로 어떤 실제 적용에서 연산들을 단일 게이트로 묶어주는 것은 매우 유용하다고 할 수 있다.