DDPM: Denoising Diffusion Probabilistic Model

DDPM이 무엇인지는 너무 유명하니 패스한다. DDPM에서 설명하는 diffusion 방식은 아래 그림과 같다.

 

먼저 DDPM은 이미지에 작은 가우시안 노이즈를 더하는 과정의 역과정 (즉 노이즈를 제거하는 과정) 역시 가우시안 분포로 모델링이 가능하다는 가정으로 시작한다. 즉 다시 말하면 normal distribution에 대한 노이즈가 주어졌을 때 이를 어떻게 복원할 것인가에 대한 문제를 모델이 해결하는 것이다.

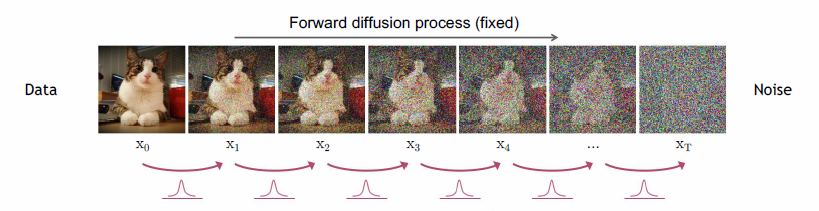
먼저 $t$ 시간 이미지 $X_t$에 노이즈 $I$를 더하는 과정의 확률분포 $q \left ( X _ { t } \mid X _ { t-1 } \right ) $는 다음과 같다.

 

$q \left ( X _ { t } \mid X _ { t-1 } \right ) = \mathcal{N}  \left ( X _ { t } ; \sqrt { 1- \beta _ { t } } X _ { t-1 } , \beta _ { t } I \right )$

 

$ \beta _ { t } $는 $t$ 시간에서 이미지에 노이즈를 얼마나 더할지에 대한 값이다. 먼저 $ \mathcal{N}  \left ( X _ { t } ; \sqrt { 1- \beta _ { t } } X _ { t-1 } , \beta _ { t } I \right )$와 같은 꼴로 표현한 이유를 간단하게 설명하자면

$Var \left ( ax \right ) =a ^ { 2 } Var \left ( x \right )$

$Var \left ( x+y \right ) =Var \left ( x \right ) +Var \left ( y \right )$

 

의 variance 성질을 사용하면 

 

$Var \left ( \sqrt { 1- \beta _ { t } } X _ { t } + \beta _ { t } \right ) =Var \left ( \left ( \sqrt { 1- \beta _ { t } } \right ) ^ { 2 } + \beta _ { t } \right ) =Var \left ( 1 \right )$

 

으로 전체 variance를 항상 1로 고정할 수 있기 때문이다. 이 값은 learnable parameter로 둘 수도 있지만, 실험을 해보니 상수로 두어도 큰 차이가 없어서 constant로 두었다고 한다. 논문에서는 $t$에따라 $10^-4$에서 $0.02$로 linear하게 증가시킨다.

 

이제 만약 최초의 이미지 $X_0$을 알고 있을때  $T$ 시간 이후의 최종 $X_T$에 대한 확률 분포  $ q\left(X_{1: T} \mid X_0\right)$ 는 다음과 같이 표현이 가능하다.

$q\left(X_{1: T} \mid X_0\right)=\prod_{t=1}^T q\left(X_t \mid X_{t-1}\right)$

 

이 수식이 만족하는 이유는 먼저

 

$q\left(x_{1: T} \mid x_0\right)=\frac{q\left(x_0, x_1, x_2, x_3, \ldots, x_T\right)}{q\left(x_0\right)}$

 

이고

 

$\prod_{t=1}^T q\left(x_t \mid x_{t-1}\right)=q\left(x_1 \mid x_0\right) q\left(x_2 \mid x_1\right) q\left(x_3 \mid x_2\right) \ldots q\left(x_T \mid x_{T-1}\right)$

 

으로 정의됨을 이용하면 Marcov chain에 의해

\begin{aligned}
& q\left(x_1 \mid x_0\right) q\left(x_2 \mid x_1\right) q\left(x_3 \mid x_2\right) \ldots q\left(x_T \mid x_{T-1}\right)=\frac{q\left(x_1, x_0\right)}{x_0} \frac{q\left(x_2, x_1\right)}{x_1} \ldots \frac{q\left(x_T, x_{T-1}\right)}{x_{T-1}} \\
& =\frac{q\left(x_1, x_0\right)}{x_0} \frac{q\left(x_2, x_1, x_0\right)}{x_1, x_0} \ldots \frac{q\left(x_T, x_{T-1}, \ldots, x_1, x_0\right)}{x_{T-1}, \ldots, x_0} \\
& =\frac{q\left(x_0, x_1, x_2, x_3, \ldots, x_T\right)}{q\left(x_0\right)}
\end{aligned}

 

임이 성립한다.

 

사실 $t$번의 sampling을 통해 매 step을 차근차근 밟아가면서 $X_0$에서 $X_t$를 만들 수도 있지만, 한 번에 $X_0$에서 $X_t$를 만들 수도 있다. 만약 $\bar{\alpha}_t=\prod_{s=1}^t\left(1-\beta_s\right)$라고 한다면

$\left.q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)\right)$

 

라고 표현되며 이를 정리하면

 

$\mathbf{x}_t=\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{\left(1-\bar{\alpha}_t\right)} \epsilon \quad \text { where } \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 

 

와 동일하다. 이 수식을 증명하자면 먼저

\begin{aligned}
& q\left(x_t \mid x_{t-1}\right) \sim N\left(x_t ; \sqrt{1-\beta_t} x_{t-1}, \beta_t I\right) \\
& \rightarrow x_t=\sqrt{1-\beta_t} x_{t-1}+\sqrt{\beta_t} \varepsilon \quad * \alpha_t=1-\beta_t, \overline{\alpha_t}=\prod_{s=1}^t \alpha_s \\
& =\sqrt{\alpha_t} x_{t-1}+\sqrt{1-\alpha_t} \varepsilon_{t-1} \\
& =\sqrt{\alpha_t}\left(\sqrt{\alpha_{t-1}} x_{t-2}+\sqrt{1-\alpha_{t-1}} \varepsilon_{t-2}\right)+\sqrt{1-\alpha_t} \varepsilon_{t-1} \\
& =\sqrt{\alpha_t \cdot \alpha_{t-1}} x_{t-2}+\sqrt{\alpha_t} \sqrt{1-\alpha_{t-1}} \varepsilon_{t-2}+\sqrt{1-\alpha_t} \varepsilon_{t-1}
\end{aligned}

 

인데 

 

\begin{aligned}
\sqrt{\alpha_t} & \sqrt{1-\alpha_{t-1}} \varepsilon_{t-2}+\sqrt{1-\alpha_t} \varepsilon_{t-1} \\
& \sim N\left(0,\left[\alpha_t\left(1-\alpha_{t-1}\right)+\left(1-\alpha_t\right)\right] I\right) \\
:= & \sqrt{\left(1-\alpha_t\right)+d_t\left(1-\alpha_{t-1}\right)}=\sqrt{1-\alpha_t \alpha_{t-1}}
\end{aligned}

 

이므로

 

\begin{aligned}
x_t=\sqrt{\alpha_t \alpha_{t-1}} x_{t-2}+\sqrt{1-\alpha_t \alpha_{t-1}} \bar{\varepsilon}_{t-2}=\sqrt{\bar{a}_t} x_0+\sqrt{1-\bar{\alpha}_t} \varepsilon \\
\therefore q\left(x_t \mid x_0\right)=N\left(x_t ; \sqrt{\alpha_t} x_0,\left(1-\bar{\alpha}_t\right) I\right)
\end{aligned}

 

로 증명이 가능하다. 달리 말하면 이론상 $\bar{\alpha}_T \rightarrow 0$ 인 경우 $\left.q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \approx \mathcal{N}\left(\mathbf{x}_T ; \mathbf{0}, \mathbf{I}\right)\right)$으로 근사할 수 있다. 한 step씩 학습을 하면 메모리와 resource가 너무 많이 들기 때문에 이렇게 한 번에 계산한다고 논문은 표현한다.

 

다음으로 노이즈로부터 이미지를 복원하는 즉 generative 과정이다. 우선 $p\left(\mathbf{x}_T\right)=\mathcal{N}\left(\mathbf{x}_T ; \mathbf{0}, \mathbf{I}\right)$라고 한다면, 임의의 $t$시간에서 $t-1$시간으로의 복원 확률 분포는 다음과 같다.

$p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \mu_\theta\left(\mathbf{x}_t, t\right), \sigma_t^2 \mathbf{I}\right)$

이때 $\mu_\theta\left(\mathbf{x}_t, t\right)$는 U-net, Denoising Autoencoder과 같은 학습 가능한 모델이다.

 

이제 학습을 적용할 차례이다. 대부분의 오토 인코더가 그렇듯 negative log likelihood를 최소화 하는 방식을 논문은 사용한다. 이를 수식으로 표현하면 다음과 같다.

 

$\mathbb{E}\left[-\log p_\theta\left(\mathbf{x}_0\right)\right] \leq \mathbb{E}_q\left[-\log \frac{p_\theta\left(\mathbf{x}_{0: T}\right)}{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}\right]=\mathbb{E}_q\left[-\log p\left(\mathbf{x}_T\right)-\sum_{t \geq 1} \log \frac{p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)}\right]=: L$

 

이를 증명하는 방법은 비교적 간단하다. 먼저 bayes rule에 의해 $p_\theta\left(x_T \mid x_0\right)=\frac{p_\theta\left(x_T, x_0\right)}{p_\theta\left(x_0\right)}$ 이므로

\begin{aligned}
& \mathbb{E}_{x_T \sim q\left(x_T \mid x_0\right)}\left[-\log p_\theta\left(x_0\right)\right]=\mathbb{E}_{x_T \sim q\left(x_T \mid x_0\right)}\left[-\log \frac{p_\theta\left(x_0, x_1, x_2, \ldots, x_T\right)}{p_\theta\left(x_1, x_2, x_3, \ldots, x_T \mid x_0\right)}\right]
\end{aligned}
이고 이 식은 

$=\mathbb{E}_{x_T \sim q\left(x_T \mid x_0\right)}\left[-\log \frac{p_\theta\left(x_0, x_1, x_2, \ldots, x_T\right)}{p_\theta\left(x_1, x_2, x_3, \ldots, x_T \mid x_0\right)} \cdot \frac{q\left(x_{1: T} \mid x_0\right)}{q\left(x_{1: T} \mid x_0\right)}\right]$

 

으로 바꿔서 표현이 가능하다. 이제 Evidence of Lower BOund (ELBO)를 적용하면 KL divergence가 양수임을 이용하여

$\leq \mathbb{E}_{x_T \sim q\left(x_T \mid x_0\right)}\left[-\log \frac{p_\theta\left(x_0, x_1, x_2, \ldots, x_T\right)}{q\left(x_{1: T} \mid x_0\right)}\right]$

 

$=\mathbb{E}_{x_T \sim q\left(x_T \mid x_0\right)}\left[-\log \frac{p_\theta\left(x_{0 ; T}\right)}{q\left(x_{1 ; T} \mid x_0\right)}\right]$

 

이다. 이제 $p_\theta\left(\boldsymbol{x}_{0: T}\right):=p_\theta\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_\theta\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right) \quad q\left(\boldsymbol{x}_{\mathbf{1}: T} \mid \boldsymbol{x}_0\right):=\prod_{t=1}^T q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)$인  Markov property를 적용하면 (어떤 시간에 특정 state에 도달하든 그 이전에 어떤 state를 거쳐왔든 다음 state로 갈 확률은 항상 같다는 성질)

\begin{aligned}
&=\mathbb{E}_{x_T \sim q\left(x_T \mid x_0\right)}\left[-\log \frac{p_\theta\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_\theta\left(\boldsymbol{x}_{\boldsymbol{t}-1} \mid \boldsymbol{x}_{\boldsymbol{t}}\right)}{\prod_{t=1}^T q\left(\boldsymbol{x}_{\boldsymbol{t}} \mid \boldsymbol{x}_{\boldsymbol{t}-1}\right)}\right]\\
&=\mathbb{E}_{x_{1: T} \sim q\left(x_{1: T} \mid x_0\right)}\left[-\log p_\theta\left(\boldsymbol{x}_T\right)-\sum_{t=1}^T \log \frac{p_\theta\left(x_{t-1} \mid x_t\right)}{q\left(x_t \mid x_{t-1}\right)}\right]
\end{aligned}

으로 증명된다. 이 loss function의 우항을 좀 더 정리하면

 

$\mathbb{E}_q[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \| p_\theta \left(\mathbf{x}_T\right)\right)}_{L_T}+\sum_{t>1} \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\right)}_{L_{t-1}} \underbrace{-\log p_\theta\left(\mathbf{x}_0 \mid \mathbf{x}_1\right)}_{L_0}]$

와 같은 최종적인 loss function을 얻을 수 있다.

이제 loss의 각각의 항에 대해 설명을 해본다. 먼저 첫 번째 항인 $L_T=D_{K L}\left(q\left(x_T \mid x_0\right) \| p_\theta \left(x_T\right)\right)$는 $p_\theta $가 생성하는 노이즈 이미지, $x_0$로부터 $q$가 생성하는 노이즈 이미지 간의 분포 차이이다. 물론 각 분포는 아래와 같이 정의된다.

\begin{aligned}
& q\left(x_t \mid x_0\right)=\mathcal{N}\left(x_t ; \sqrt{\bar{\alpha}_t} x_0,\left(1-\bar{\alpha}_t\right) \mathrm{I}\right) \\
& p_\theta\left(x_T\right)=\mathcal{N}\left(x_T ; 0, \mathrm{I}\right)
\end{aligned}

 

하지만 일반적으로 $q\left(x_T \mid x_0\right)=p_\theta\left(x_T\right)$이기 때문에 (이를 위해 논문은 $\beta_t$를 상수로 둔다.) 이 loss term은 항상 0에 가까운 상수이며, 학습과정에서 무시된다.

 

두 번째로 $L_{T-1}$는  $p_\theta$와 $q$ 의 reverse, forward process의 분포 차이를 의미한다. 모델은 이들을 최대한 비슷하게 만드는 방향으로 학습된다. $p_\theta$는 모델 출력 부분이니 넘어가고  $q\left(x_{t-1} \mid x_t, x_0\right)$은 $P\left(x_{t-1} \mid x_t\right)=\frac{P\left(x_t \mid x_{t-1}\right) P\left(x_{t-1}\right)}{P\left(x_t\right)}$를 이용하면 $q\left(x_{t-1} \mid x_t, x_0\right)=q\left(x_t \mid x_{t-1}, x_0\right) \frac{q\left(x_{t-1} \mid x_0\right)}{q\left(x_t \mid x_0\right)}$임을 알 수 있다. 마지막으로 역 조건부 확률(inverse conditional probability)에 의해

 

$q\left(x_{t-1} \mid x_t, x_0\right)=N\left(x_{t-1} ; \tilde{\mu}\left(x_t, x_0\right), \tilde{\beta}_t \mathrm{I}\right)$

 

\begin{aligned}
& \tilde{\mu}_t\left(x_t, x_0\right):=\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} x_0+\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha} t} x_t, \tilde{\beta}_t:=\frac{\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \beta_t
\end{aligned}

로 계산할 수 있다.

이제 $L_{T-1}$의 KL divergence를 계산하면

 

$L_{t-1}=\mathbb{E}_{\mathbf{x}_0 \sim q\left(\mathbf{x}_0\right), \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\left[\frac{\beta_t^2}{2 \sigma_t^2\left(1-\beta_t\right)\left(1-\bar{\alpha}_t\right)}\left\|\epsilon-\epsilon_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \epsilon, t\right)\right\|^2\right]$

 

로 가능하다.

 

마지막으로 $L_0$는 $x_1$으로부터 $x_0$를 추정하는 likelihood이다. 모델은 이를 maximize하는 방향으로 학습된다.

 

이제 전체 loss function을 epsilon에 대한 식의 형태로 simplify가 가능한데 simplify 된 형태가 더 학습이 잘된다고 한다. 식은 다음과 같다.

 

$L_{\text {simple }}(\theta):=\mathbb{E}_{t, \mathbf{x}_0, \boldsymbol{\epsilon}}\left[\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2\right]$

 

따라서 학습 부분은 아래와 같이 간단하게 표현된다.

 

반대로 이미지 생성 (sampling 부분은)

와 같이 표현된다.