Taming Transformers for High-Resolution Image Synthesis

VQ-GAN을 이해하기 위해서는 VAE(Variational Auto-Encoder)와 VQ-VAE에 대한 지식이 필요하다.

 

1. VAE

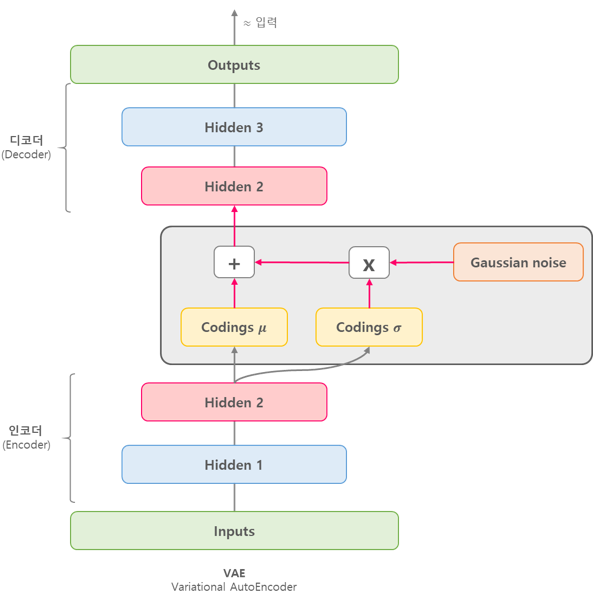
VAE의 대략적인 구조는 위와 같다. Input image $x$를 인코더에 통과시켜 latent vector $z$를 생성하고, $z$를 다시 디코더에 통과시켜 기존 input $x$와 비슷하지만 새로운 이미지 $x$를 찾아내는 구조이다. 그렇다면 auto-encoder와의 차이점은 무엇인가?

위 그림과 같이 auto-encoder는 특정 입력 이미지를 잘 임베딩 하여 원본 이미지로 복원하는 과정을 학습한다. 즉 feature 추출과 압축을 위한 과정을 학습한다. 반면 VAE는 어떠한 latent space가 원하는 이미지를 만들어 내는지 그 확률 분포를 학습한다. 즉 새로운 이미지 생성을 위한 모델이다.

 

 

결과적으로 latent space의 "분포"가 중요하기 때문에 VAE의 인코더는 입력 이미지 $x$를 인코딩한 확률 분포 $q_\phi(\mathbf{z} \mid \mathbf{x})$의 평균 $\mu$와 표준편차 $\sigma$의 값을 학습한다. 반대로 디코더는 latent space $z$를 다시 input $x$로 변환하는 역할을 한다. 만약 입력 이미지로부터 생성된 $z$를 그대로 사용한다면 VAE는 언제나 입력 이미지와 동일한 이미지만 생성이 가능할 것이다. 이러한 문제를 해결하기 위해 가우시안 분포 $N(O,I)$ 를 따르는 노이즈 $\epsilon$을 샘플링하여 새로운 latent space $\mathrm{z}=\mu+\sigma^2 \cdot \epsilon$를 생성한다. 이러한 방법을 

reparametererization trick이라고 부르는데, 사실 노이즈를 샘플링하는 과정은 미분이 불가능하기 때문에 학습을 위해 $z$를 이러한 형태로 표현하는 것이다. 결과적으로 디코더는 latent vector $z$가 주어졌을 때 $x$의 분포 $p_\theta(\mathbf{x} \mid \mathbf{z})$를 approximate하는 것을 목적으로 한다. $z$ 주어짐에 따라 다시 데이터 $x$를 generate하는 역할을 하기 때문에 디코더가가 generative model의 역할을 하게 된다.

 

이제 VAE를 학습하기 위해 maximum likelihood를 적용한다. 이를 수식으로 표현하면 다음과 같다. (마지막 줄은 KL divergence의 정의를 활용한다.)

$$
\begin{aligned}
\log p_\theta(\mathbf{x}) & =\int q_\phi(\mathbf{z} \mid \mathbf{x}) \log p_\theta(\mathbf{x}) d \mathbf{z} \\
& =\int q_\phi(\mathbf{z} \mid \mathbf{x}) \log \frac{p_\theta(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z})}{p_\theta(\mathbf{z} \mid \mathbf{x})} d \mathbf{z} \\
& =\int q_\phi(\mathbf{z} \mid \mathbf{x}) \log \frac{p_\theta(\mathbf{x} \mid \mathbf{z}) p(\mathbf{z})}{p_\theta(\mathbf{z} \mid \mathbf{x})} \frac{q_\phi(\mathbf{z} \mid \mathbf{x})}{q_\phi(\mathbf{z} \mid \mathbf{x})} d \mathbf{z} \\
& =\int q_\phi(\mathbf{z} \mid \mathbf{x}) \log p_\theta(\mathbf{x} \mid \mathbf{z}) d \mathbf{z}-K L\left(q_\phi(\mathbf{z} \mid \mathbf{x}) \| p(\mathbf{z})\right)+K L\left(q_\phi(\mathbf{z} \mid \mathbf{x}) \| p_\theta(\mathbf{z} \mid \mathbf{x})\right)
\end{aligned}
$$

 

마지막 식에서 첫째 항은 인코더로부터 $z$를 sampling하고, 다시 이 $z$로부터 디코더를 활용해서 $p_\theta(\mathbf{x} \mid \mathbf{z})$를 계산함으로써 구할수 있다. 그리고 두 번째 항은 $q$와 $p$가 둘 다 정규분포이기 때문에, 정규분포 두 개 사이의 KL divergence는 쉽게 계산이 가능하다. 하지만 세 번째 항은 우리가 $p_\theta(\mathbf{z} \mid \mathbf{x})$ 를 알 수가 없기 때문에 계산하는 것이 불가능하다. 하지만 우리는 KL divergence가 항상 양수라는 것을 안다. 그래서 우리는 마지막 식을 다음과 같은 부등식으로 표현할 수 있다. 이것이 그 유명한 (evidence lower bound, ELBO이다.)

 

$$
\begin{aligned}
& =\int q_\phi(\mathbf{z} \mid \mathbf{x}) \log p_\theta(\mathbf{x} \mid \mathbf{z}) d \mathbf{z}-K L\left(q_\phi(\mathbf{z} \mid \mathbf{x}) \| p(\mathbf{z})\right)+K L\left(q_\phi(\mathbf{z} \mid \mathbf{x}) \| p_\theta(\mathbf{z} \mid \mathbf{x})\right) \\
& \geq \int q_\phi(\mathbf{z} \mid \mathbf{x}) \log p_\theta(\mathbf{x} \mid \mathbf{z}) d \mathbf{z}-K L\left(q_\phi(\mathbf{z} \mid \mathbf{x}) \| p(\mathbf{z})\right) \longleftarrow \text { Evidence lower bound (ELBO) }
\end{aligned}
$$

 

2. VQ-VAE (Vector Quantization Variational Auto Encoder)

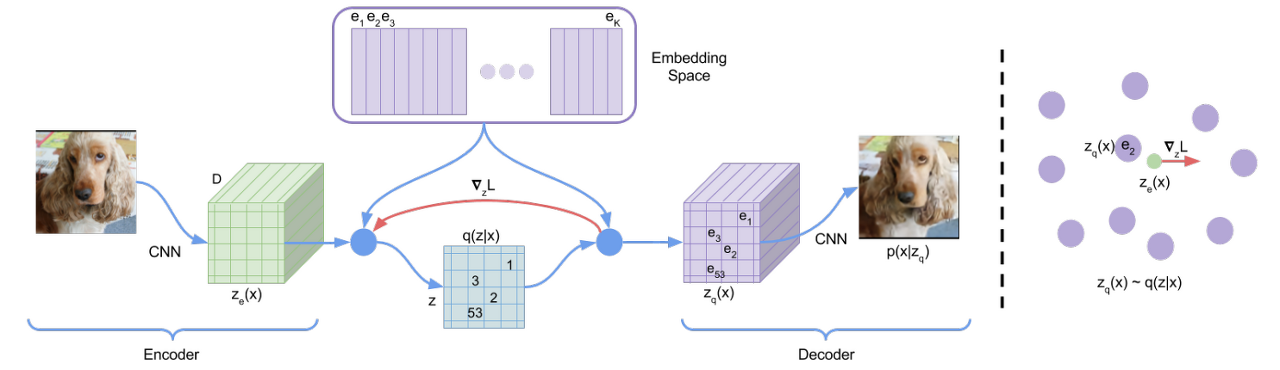
위 그림과 같이 VQ-VAE는 기존 VAE에 discrete 한 codebook을 추가한 버전이다. 인코더의 출력으로 어떤 벡터가 나오면, codebook의 모든 벡터들 간 거리를 계산한다. Codebook의 벡터들 중 인코더의 출력 벡터와 가장 거리가 짧은 벡터를 찾고, 그 벡터를 디코더에 넣어 학습하는 구조이다. 위 그림을 참고하면 다음과 같은 수식으로 계산된다.

$z_q(x)=e_k, \quad \text { where } \quad k=\operatorname{argmin}_j\left\|z_e(x)-e_j\right\|_2$

 

문제는 위 식이 미분 불가능함으로 gradient를 계산할 수 없다는 것이다. 대신 straight-through estimator와 비슷한 방법을 사용하여 gradient를 근사할 수 있다. 좀 더 자세히 설명하면 디코더 입력인 $z_q(x)$의 gradient를 인코더의 출력 쪽으로  gradient 복사하면 된다는 것이다. 따라서 전체 loss function은 다음과 같다.

 

$L=\log p\left(x \mid z_q(x)\right)+\left\|\operatorname{sg}\left[z_e(x)\right]-e\right\|_2^2+\beta\left\|z_e(x)-\operatorname{sg}[e]\right\|_2^2$

 

첫 번째 항은 reconstruction loss로 위에서 설명한 estimator를 통해 decoder와 encoder를 모두 최적화한다. 임베딩 $e_i$는 어떤 gradient도 받지 못하기 때문에 Vector Quantisation(VQ)를 사용한다. 두 번째 항의 VQ objective는 각 $e$를 인코더의 출력 $z_e(x)$로 이동하게끔 한다. 마지막으로 embedding space는 무한하기 때문에  $e_i$ 는 인코더 parameter만큼 빠르게 학습되지 않을 수 있다. 인코더가 embedding과 출력이 grow할 수 있게 만들기 위해 3번째 항 commitment loss를 추가한다.

 

3. VQ-GAN

 

마지막으로 VQ-VAE의 GAN 확장 버전인 VQ-GAN의 구조는 위와 같다. 그림과 같이 VQ-GAN은 VQ-VAE와 거의 동일한 구조를 가지지만 몇가지 차이점이 있다.

1. VQ-VAE와 달리 adversarial learning을 사용하여 학습을 진행한다. VQ-VAE 처럼 Encoder에서 나온 vector 값과 codebook 간의 유클리디안 distance를 비교한 후 distance가 가장 작은 vector 들의 값으로 quantized vector를 구성한다. 이렇게 생성한 feature를 디코더에 넣어 reconstruction image를 생성한다. 그리고 이를 discriminator에 넣어 patch 단위로 real인지 fake인지 판단한다.
2. Code book에 transformer를 추가하여 codebook의 index를 전에 나왔던 값을 기반으로 auto-regressive 하게 예측한다. $i$ 번째 보다 작은 값들을 이용하여 $i$ 번째의 index를 예측하는 것이다. 따라서 이렇게 예측한 $i$ 번째 index 값을 codebook 과 mapping 하여 생성하는 이미지 다음 patch vector를 구성한다. 

위와 같이 구성된 이유는 일반적으로 CNN은 local 정보에, transformer는 global 정보에 특화 되어있기 때문에 CNN을 통해 각 영역별 $z$를 추출하고 transformer로 전체 순서를 예측한다.

VQ-GAN의 loss function은 아래와 같다. VQ-VAE와 거의 동일하다.

 

\begin{aligned}
\mathcal{L}_{\mathrm{VQ}}(E, G, \mathcal{Z})=\|x-\hat{x}\|^2 & +\left\|\operatorname{sg}[E(x)]-z_{\mathbf{q}}\right\|_2^2+\beta\left\|\operatorname{sg}\left[z_{\mathbf{q}}\right]-E(x)\right\|_2^2
\end{aligned}

 

GAN loss는 다음과 같다.

 

$\mathcal{L}_{\mathrm{GAN}}(\{E, G, \mathcal{Z}\}, D)=[\log D(x)+\log (1-D(\hat{x}))]$

 

따라서 전체 loss는 다음과 같다.

 

\begin{aligned}
& \mathcal{Q}^*=\underset{E, G, \mathcal{Z}}{\arg \min } \max _D \mathbb{E}_{x \sim p(x)}\left[\mathcal{L}_{\mathrm{VQ}}(E, G, \mathcal{Z})+\lambda \mathcal{L}_{\mathrm{GAN}}(\{E, G, \mathcal{Z}\}, D)\right]
\end{aligned}

 

이때 $\lambda$는 adaptive weight로 두 loss 간의 균형을 맞추는 값이다. 이는 다음과 같이 정의된다.

 

 

$\lambda=\frac{\nabla_{G_L}\left[\mathcal{L}_{\mathrm{rec}}\right]}{\nabla_{G_L}\left[\mathcal{L}_{\mathrm{GAN}}\right]+\delta}$