-
Lasso Regression #1머신러닝 기초 2019. 10. 9. 12:14반응형
만약 모델을 학습할 때 입력되는 feature수가 너무 많다면 (예를 들어 Lot size, Single Family, Year built, Last sold price, Last sale price/sqft, Finished sqft, Unfinished sqft 등등) 효율성 측면에서 불리하다.

만약 feature selection을 통해 우리가 필요한 feature만 추출하여 weight를 sparse(0이 많이 포함된 것)하게 만들 수 있다면 좀 더 효율적으로 학습할 수 있을 것이다.
그렇다면 어떻게 feature selection을 할 수 있을까? 가장 간단한 방법은 모든 경우의 수를 고려해보는 것이다.

문제는 고려해야 할 feature의 개수가 늘어나면 경우의 수가 기하급수적으로 증가해 실질적으로 이를 계산하는 것은 불가능에 가깝다. 또 다른 방법으로 greedy algorithm도 있는데 여기서는 다루지 않겠다.
가장 효율적으로 feature selection을 하는 방법은 regularization을 이용하는 것이다. 우선 앞서 설명했던 ridge regression의 cost function은 다음과 같다.
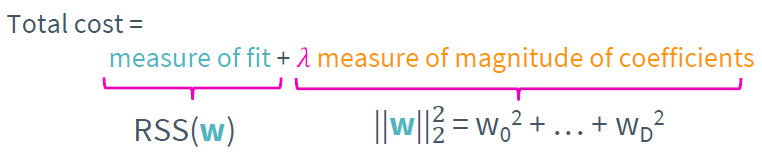
lambda가 커질수록 weight는 0으로 수렴함을 알고 있다. 만약 특정한 lambda에서 weight가 크다면 그 feature 우리의 모델과 상관관계가 크다는 것이며 반대로 weight가 작다면 상관관계가 작다는 것을 의미한다. 따라서 적당한 threshold를 잡아 threshold 이상의 weight를 가지는 feature만 선택하면 쉽게 feature selection을 할 수 있다.
집값 예측을 예로 들어보자.
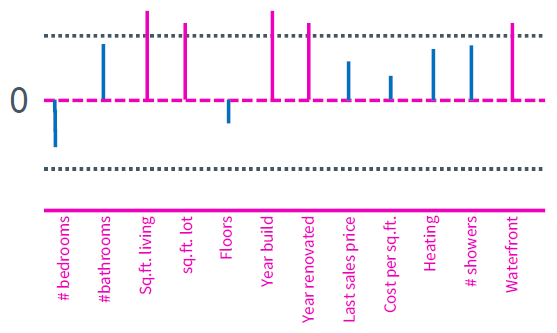
보라색의 feature들이 threshold를 넘는 즉 selection 된 feature들이다. 하지만 여기서 주목해야 할 점이 있다. 아래 그림을 고려해보자.

bathroom의 개수와 shower의 개수는 모두 threshold 이하이지만 비슷한 weight를 가짐을 알 수 있다. 집값을 예측하는데 bathroom의 개수는 분명히 중요한 feature이지만 여기서는 고려되지 못했다. 사실 bathroom의 개수와 shower의 개수는 밀접한 관련이 있다. bathroom에는 반드시 shower가 존재할 테니 동일한 feature라고 봐도 무방하다. 이러한 중복된 feature가 regularization을 이용한 feature selection의 큰 문제로 작용한다. 만약 shower라는 feature를 제거했다면 아래와 같이 bathroom은 정상적으로 selection이 되었을 것이다. (모델이 선형적이기 때문이다.)

우리는 w가 sparse 함을 원했지만 ridge regression은 wight를 전체적으로 작게 만들어 위와 같은 문제를 발생시킨다. 즉 몇 개의 큰 weight 보다는 전체적으로 작은 weight를 선호하기 때문에 ridge regression은 feature selection에 그리 좋은 방법이 아니다.
이제 lasso regression을 고려해보자 lasso regression의 cost function은 다음과 같다.

lasso regression은 weight를 sparse 하게 만들기에 매우 적합하다. 이 이유를 설명하기 전에 lambda에 따른 weight의 변화는 아래와 같다.

ridge와 lasso의 차이점은 그래프에서 극명하게 드러난다. 우선 ridge의 경우

lambda가 증가함에 따라 모든 feature의 weight가 0을 향해 감소하며 0에 무한히 수렴할 뿐 완전히 0에 도달하지는 못했다. 하지만 lasso의 경우

lambda가 증가함에 따라 모든 feature의 weight가 0을 향해 감소하기는 하나 0에 도달하는 위치가 다르며 0에 완전히 도달한다. 따라서 특정한 lambda에서 weight의 sparse함이 보장된다.
반응형'머신러닝 기초' 카테고리의 다른 글
Lasso Regression #3 (0) 2019.10.11 Lasso Regression #2 (0) 2019.10.09 Ridge Regression #2 (0) 2019.10.05 Ridge Regression #1 (0) 2019.10.03 Bias-Variance Trade Off (0) 2019.09.29