-
Ridge Regression #1머신러닝 기초 2019. 10. 3. 18:05반응형
앞선 글들에서 regression의 차수가 증가하면 모델이 데이터에 overfit 되는 문제를 다뤘다.

또한 overfitting은 매우 큰 regression coefficient 때문에도 발생한다. 그렇다면 overfitting과 데이터수, input과의 관계는 어떨까?
우선 일반적인 regression model은 아래와 같다.

만약 아래와 같이 관측된 데이터수가 많다면 overfitting은 쉽게 일어날 것이며 데이터수가 적다면 overfitting이 일어나기 어려울 것이다.

만약 input(집값을 예로 들면 침대 개수, 화장실 개수, 거실 크기 등등)이 많다면 역시나 아래와 같이 overfit 되기 어려울 것이다.

Overfitting 문제를 해결할 수 있는 또 다른 방법은 Cost function에 새로운 항을 추가하는 것이다. 지금까지 사용한 cost function은 아래와 같다.
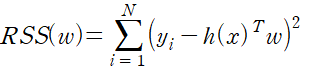
이제 이 함수에 Regularization항을 추가하여 overfit을 방지할 수 있으며 주로 L1 또는 L2 Regularization을 사용한다 각각 아래와 같이 표현되는 식이다.

이때 L2를 사용하면 Ridge regression, L1을 사용하면 LASSO regression이라 한다. 따라서 새로운 cost function은
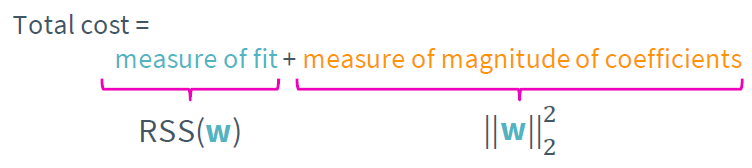
이다. 물론 아래와 같이 regularization항 앞에 상수를 곱하여 사용한다.

이때 이 상수를 tuning parameter이라 부르며 모델의 복잡도를 조절하는 역할을 한다. 이제 tuning parameter의 크기에 따라 주어진 cost function이 최소가 되는 weight를 계산해보자. 만약 tuning parameter가 0이라면

이며 LS는 least squares(최소제곱법)이다. 만약 tuning parameter가 무한대라면
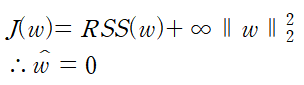
이므로 나머지 경우는
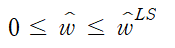
이다.
만약 tuning parameter의 크기가 크다면 큰 bias에 작은 variance이며 tuning parameter가 작다면 작은 bias에 큰 variance를 가진다.
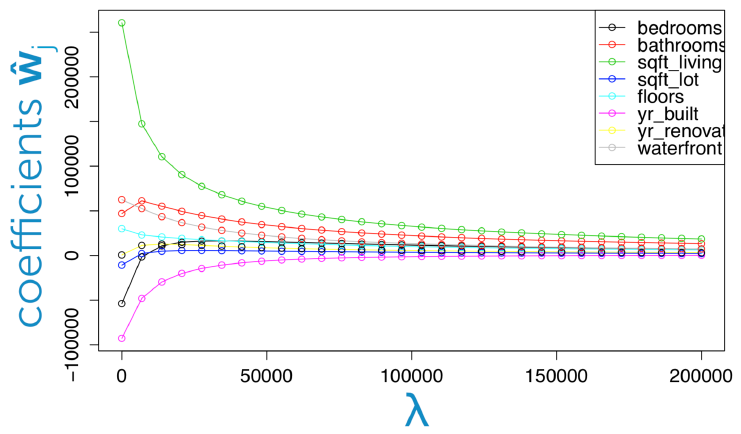
위의 그래프는 tuning parameter의 크기에 따라 각 feature의 weight의 coefficient의 변화를 나타낸 것이다. tuning parameter가 작을수록 모델이 overfit 되어 coefficient의 절댓값이 큰 반면 tuning parameter이 크면 coefficient의 크기가 작아짐을 확인할 수 있다.
이제 실제로 ridge regression을 구현해보자. 우선 RSS를 행렬 곱으로 표현하면 아래와 같았다.

수식으로 표현하면
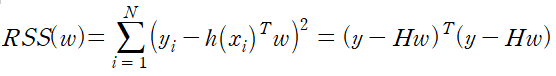
또한 L2 regularization 항은 아래와 같이 표현된다.

이제 전체식은

이다.
이제 이 ridge regression cost의 gradient를 계산해보자.
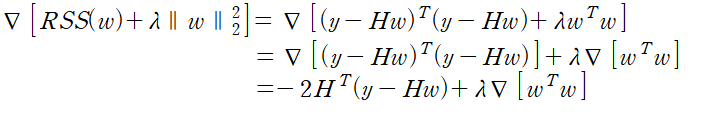
오른쪽 첫째 항의 gradient는 이미 앞선 내용에서 보였다. 두 번째 항을 계산하기 위해

라고 하면
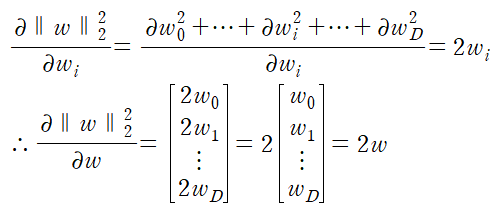
이다. 따라서 ridge regression cost의 gradient는

이다. 이제 gradient가 0인 지점을 찾기 위해

을 계산하면 된다. (I는 identity matrix이다.) 따라서

이며 이 결과는 closed-form solution이다. 이때 만약 lambda가 0이라면
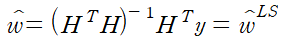
이다.

역행렬 계산 시 시간 복잡도가 세제곱이므로 실제로는 거의 쓰이지 않는다.
역시 이 문제를 해결하기 위해 gradient descent를 이용한다.

에서 https://hydragon-cv.info/entry/Fitting-the-linear-regression-model?category=817047와 동일하게 계산하면

이다.
이때 learning rate와 regulaization parameter lambda를 hyperparameter(machine learning 학습을 할 때에 더 효과가 좋도록 하는 자동 설정되는 변수를 의미한다.)라고 한다.
반응형'머신러닝 기초' 카테고리의 다른 글
Lasso Regression #1 (0) 2019.10.09 Ridge Regression #2 (0) 2019.10.05 Bias-Variance Trade Off (0) 2019.09.29 Assessing Performance (0) 2019.09.28 Numerical vs. analytic gradients (0) 2019.09.23