Lasso Regression #2

이제 lasso regression을 실제로 적용해보자. 앞선 ridge regression과 마찬가지로 closed-form solution과 gredient descent 알고리즘 2가지 방식을 이용한다.

 

lasso의 total cost는 다음과 같다.

 

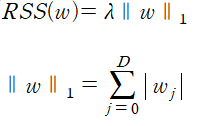
따라서 closed-form을 위해서는 |w|의 derivative(도함수)가 필요하다. 이를 그래프로 표시하면 다음과 같다.

 

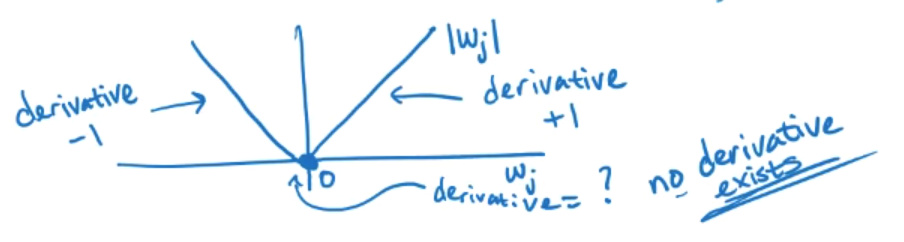
문제는 원점에서의 도함수가 존재하지 않다는 것이다. 따라서 lasso regression의 closed-form solution은 존재하지 않는다.

 

이제 다른 방식을 이용해보자 lasso에서는 coordinate descent라는 새로운 방식을 이용한다.(위의 도함수 문제로 기존의 gredient descent를 사용하지 못한다.) coordinate descent의 목표는 아래와 같이 정의된 함수 g를 최소화하는 것이다.

 

g와 같은 다변수 함수를 한 번에 최적화하는 것은 매우 어렵기 때문에 한 변수(예를 들어 j번째)를 제외한 나머지 변수를 고정시켜 둔 뒤, 한 변수에 대해서만 최적화할 수 있다. 이를 수식으로 표현하면

 

와 같다. 아래 그림과 같이 w0, w1 2개의 차원에 대해서 고려해보자

 

예를 들어 가로축을 w0, 세로축을 w1이라 할 수 있을 것이다. 매 iteration마다 w0, w1을 반복해서 고정하고 고정되지 않은 값을 최적화하면 위와 같이 계단 형태의 그래프가 될 것이다.

 

물론 이 경우에는 차원이 2개이므로 번갈아 가며 좌표축을 선택했지만 다차원의 경우 다음 좌표축을 결정할 기준이 필요할 것이다. 만약 다음 좌표축을 random 하게 선택하면 random (혹은 stochastic) coordinate descent가 되며 round robin 방식을 사용할 수도 있다. 중요한 점은 이 방식은 step size를 결정할 필요가 없으며(gradient decent와 대조적이다.) 여러 문제를 해결하는데 아주 유용한 방법이라는 것이다.

 

이제 coordinate descent의 과정을 자세히 알아보자. 우선 각각의 feature들을 normalizing 하는 과정을 거친다.

 

nomalized 된 feature의 원소들은 아래와 같은 이유에 의해 다음의 식을 만족함을 기억하자.

 

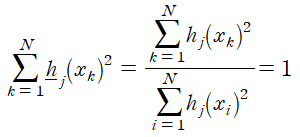
아래 그림에 적용시켜 보면 각 feature에 대해 N개의 데이터가 있고 j는 0에서 D까지의 값을 가진다. normalizing은 test set에도 동일하게 적용된다.

 

이제 최적화를 위해 RSS를 계산하면 다음과 같다.

 

이제 wj를 제외한 나머지 weight를 고정하고 RSS가 최소인 점을 찾기 위해 편미분 하면

 

이다. 이때

 

라고 정의하면 결과적으로

 

 이다. 따라서

 

이다. 이제 coordinate descent의 전체적인 과정을 설명하면 다음과 같다. 우선 weight를 초기화 한 뒤에 j를 0 ~ D로 증가시키며

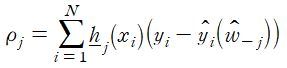
를 계산한다. (w_-j는 j번째 weight를 제외한 나머지 weight이다.) 마지막으로

 

로 설정하면 coordinate descent 알고리즘이 완성된다.

 

지금까지 계산한 것은 RSS만 고려하였으므로 lasso가 아닌 mean squares를 위한 coordinate descent이다. lasso에 적용된 coordinate descent는 아래와 같다.

 

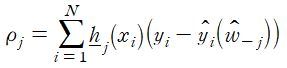
이러한 방식을 soft thresholding라고하며 이 구조에 의해 weight의 sparse 함이 제대로 드러난다. 그래프로 표현한다면 다음과 같다.

 

 

lasso의 경우 feature와 모델의 상관관계가 특정 이하면 weight가 완전히 0이 된다. 이것은 왜 lasso가 feature selection을 수행하는지에 대한 이유이다.

 

이제 최종적인 lasso의 coordinate descent 알고리즘은 아래와 같다.

 

참고로 학습을 중단하는 기준은 coordinate descent의 한 스텝이 특정 값 이하로 감소하면 수렴한다고 하는 것이 일반적이다.

 

Feature가 unnormalized 된 경우 coordinate descent 알고리즘은 아래와 같이 약간 다르다. 강조된 부분의 차이점에 주목하자.