-
Geometric intuition of solution머신러닝 기초 2019. 10. 12. 23:09반응형
지금까지 본 regression의 2가지 방법인 ridge와 lasso를 그래프를 이용해 표현해보겠다. 우선 편의를 위해 2개의 feture와 weight(w0, w1)을 가지는 모델을 고려해보자. 우선 ridge의 경우 cost function이 아래와 같음을 상기하자.

빨간색 부분과 초록색 부분을 나누어서 생각해보자. 우선 빨간색 부분을 전개하면
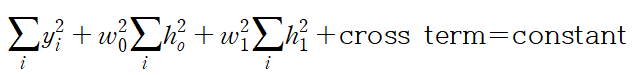
이런 형태이므로 w0와 w1에 대해 타원의 방정식이다. 좌표평면 위에 표현하면 다음과 같다.
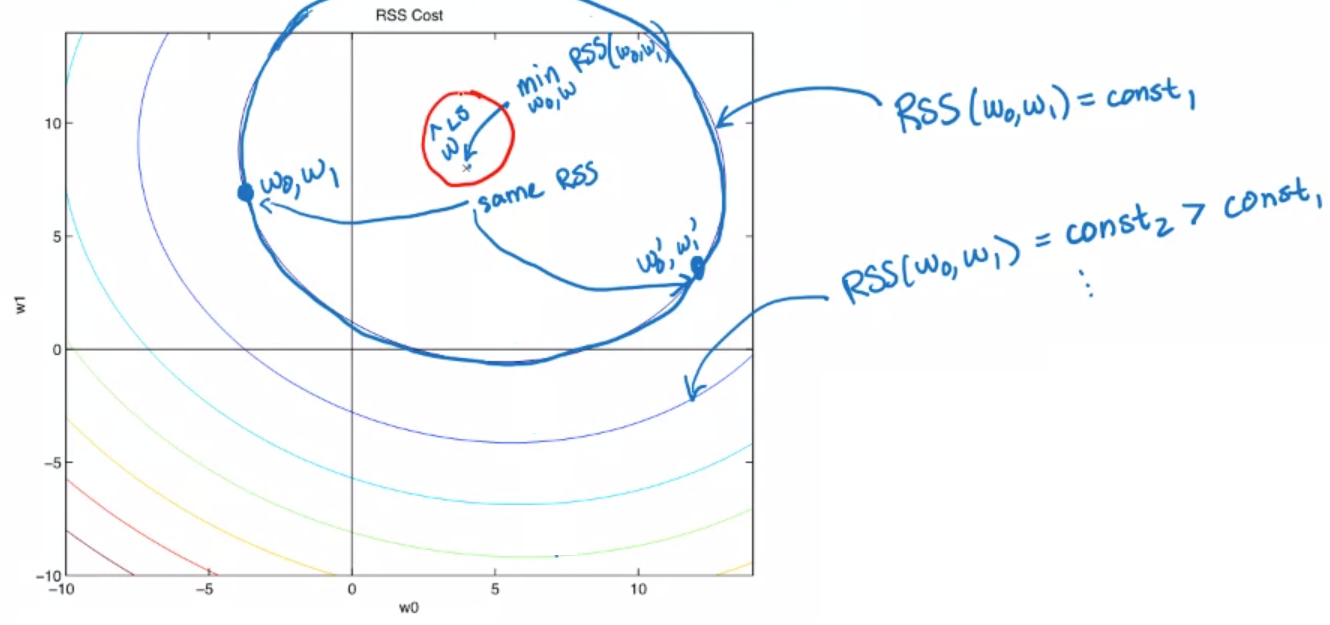
등고선과 비슷한 같은 타원 위의 점들은 모두 동일한 RSS를 가진다. 타원의 크기가 작을수록 RSS의 값도 작아지며 결과적으로 타원의 중심에서 최소의 least square RSS를 가진다.
이제 초록색 부분을 고려해보자. 초록색 부분은 쉽게 원의 방정식임을 알 수 있다. 좌표평면 위에 표현하면 다음과 같다.

동일한 원위의 점은 동일한 L2 norm을 가진다. 원의 반지름이 작을수록 L2 norm의 크기도 작아지며 결과적으로 원의 중심에서 최소의 L2 norm을 가진다.
초록색과 빨간색 부분을 동시에 고려하면 결과적으로 타원의 방정식이 될 것이다. 그렇다면 lambda가 커질수록 그래프의 모양은 어떻게 바뀔까? 아래 시뮬레이션 결과가 있다.

lambda의 크기가 커질수록 cost가 최소가 되는 지점 (타원의 중심)이 원점에 수렴함을 알 수 있으며 이 결과는 ridge regression에서 lambda의 크기가 커지면 weight가 0에 수렴함과 동일하다.
참고로 특정 lambda에 대해 ridge cost의 최적의 solution이 존재하는데 아래 그림과 같이 L2 norm과 RSS의 교점에 해당하는 부분이다. 만약 더 큰 lambda를 선택하면 solution의 위치도 이동한다.

이제 lasso에 대해서도 계산해보자. lasso의 경우 cost function이 아래와 같다.

빨간색 부분은 앞서 계산한 ridge와 동일하므로 생략한다. 이제 초록색 부분은 쉽게 마름모 형태임을 알 수 있다. 그래프로 나타내면 다음과 같다.

동일한 마름모 위의 점들은 L1 norm의 크기가 같으며 마름모의 중심은 L1 norm의 크기가 최소인 지점이다. lasso 역시 초록색과 빨간색 부분을 동시에 고려하면 결과적으로 타원의 방정식이 될 것이다. lambda가 커질수록 그래프의 모양은 아래와 같이 변화한다.
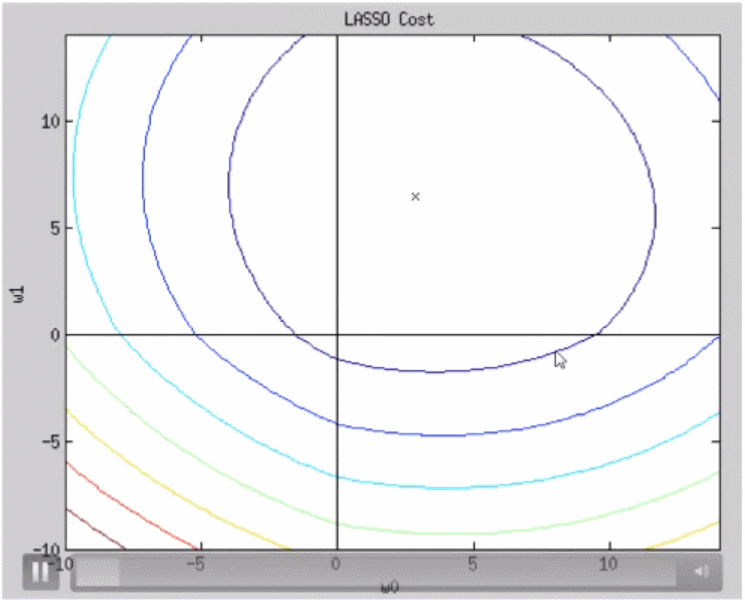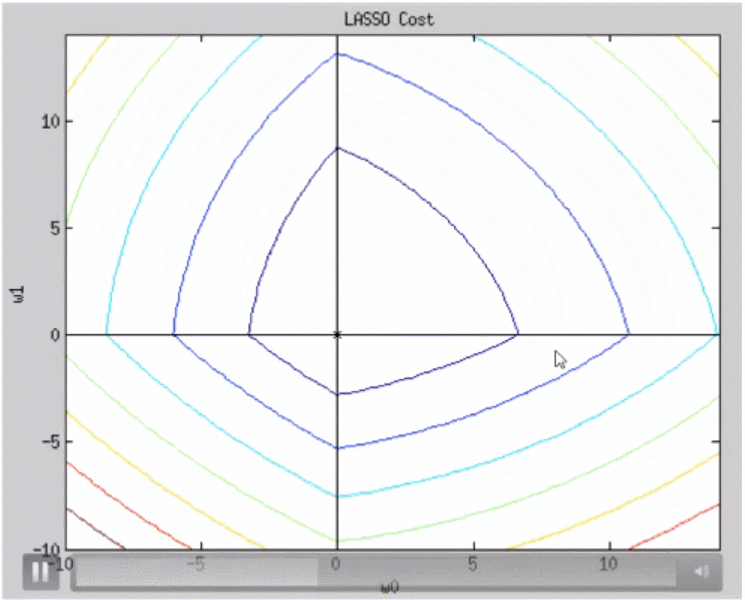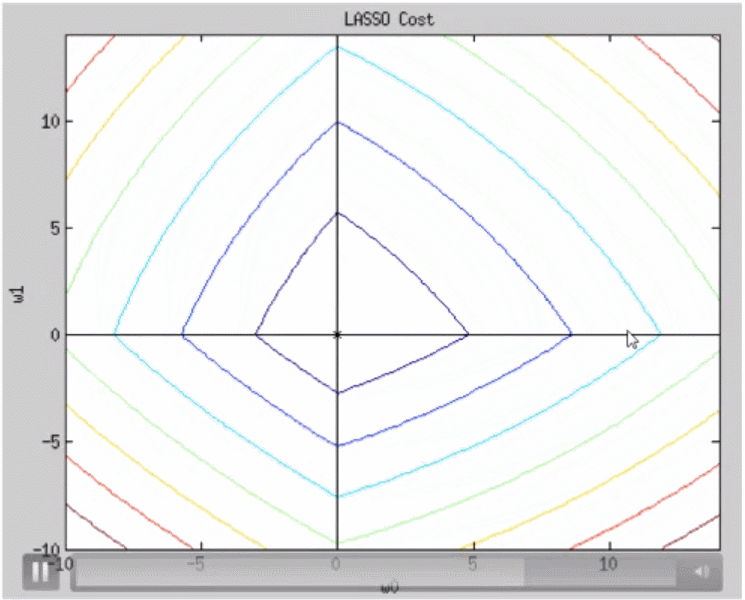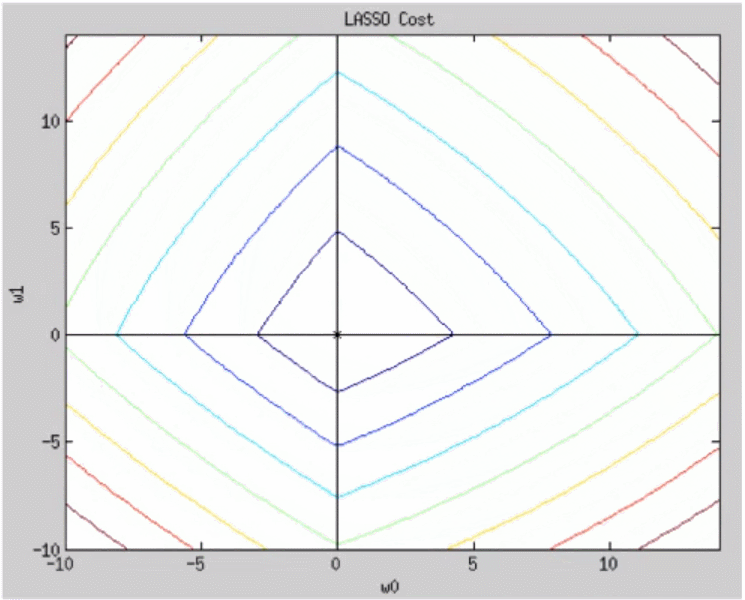
w0, w1 모두 0에 수렴하는 것은 동일하지만 ridge와 달리 2개의 축 중 하나가 먼저 0에 도달함을 알 수 있다. 그 이유는 아래 그래프로 설명이 가능하다.

특정 lambda에 대해 ridge cost의 최적의 solution은 위의 그림과 같이 L1 norm과 RSS의 교점에 해당하는 부분이다. 마름모와 타원의 교점이므로 교점은 마름모의 꼭짓점에 형성될 가능성이 높다. 이러한 특징에 의해 weight의 sparse 함이 성립되며 이를 기하학적으로 설명했다.
반응형'머신러닝 기초' 카테고리의 다른 글
Logistic regression #2 (0) 2019.11.03 Logistic regression #1 (0) 2019.11.02 Lasso Regression #3 (0) 2019.10.11 Lasso Regression #2 (0) 2019.10.09 Lasso Regression #1 (0) 2019.10.09