-
Logistic regression #1머신러닝 기초 2019. 11. 2. 23:45반응형
지금까지의 모델들과 달리 일종의 좋고 나쁨을 결정하는 모델을 만든다고 가정하자. 예를 들어 식당에 대한 리뷰글을 통해 좋은 식당인지(+1), 나쁜 식당인지(-1) 판단하는 모델 일수 있다.

이렇게 특정 클래스로 분류하는 모델을 Linear classifier이라 한다.
식당을 예로 들면 리뷰글에 awesome, awful 등의 단어수가 식당의 좋고 나쁨(predicted class)를 결정하는 중요한 요소가 될 것이며 이러한 요소들을 이용해 리뷰글의 점수(score)를 결정할 수 있을 것이다.
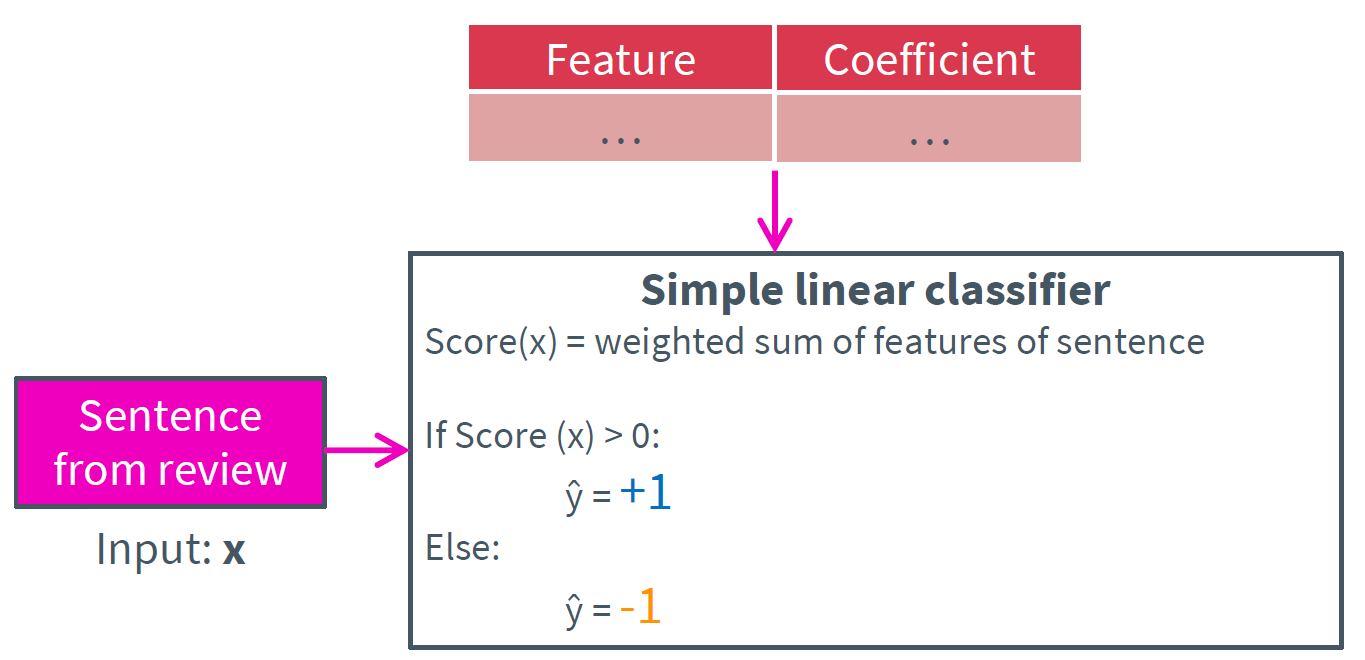
결국 우리의 linear classifier는 이 점수에 따라 점수가 0보다 크다면 predict는 +1(좋은 식당), 0보다 작다면 -1(나쁜 식당)으로 결정되게 할 수 있을 것이며 이것이 linear classifier의 기본 아이디어이다.
물론 리뷰글에 포함된 각 단어마다 식당을 판단하는데 영향을 미치는 가중치(계수)가 다를 것이다. 예를 들어 긍정의 단어일수록 그 계수가 크며 부정의 단어일수록 그 계수가 작을 것이다.
그렇다면 2개의 단어(awesome, awful)에 대해 리뷰글을 분류해보자. 이때 awesome의 계수는 1.0, awful의 계수는 -1.5이다. 그래프로 표현하면 다음과 같다.
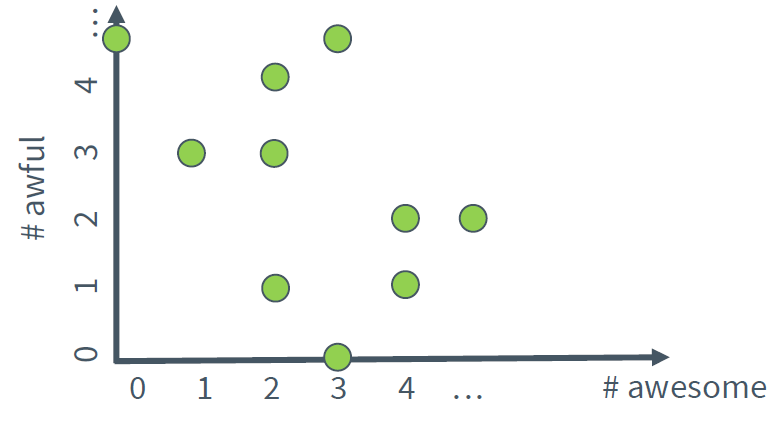
여러 리뷰글을 글에 포함된 awesome과 awful의 단어수에 따라 좌표평면 위에 표현한 것이다. 이제 각 글의 점수를 구하기 위해 아래와 같은 선형식을 이용하자.
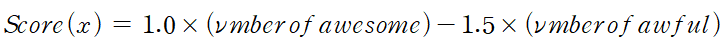
이제 좌표평면 위에 score가 0인 지점을 선으로 그으면
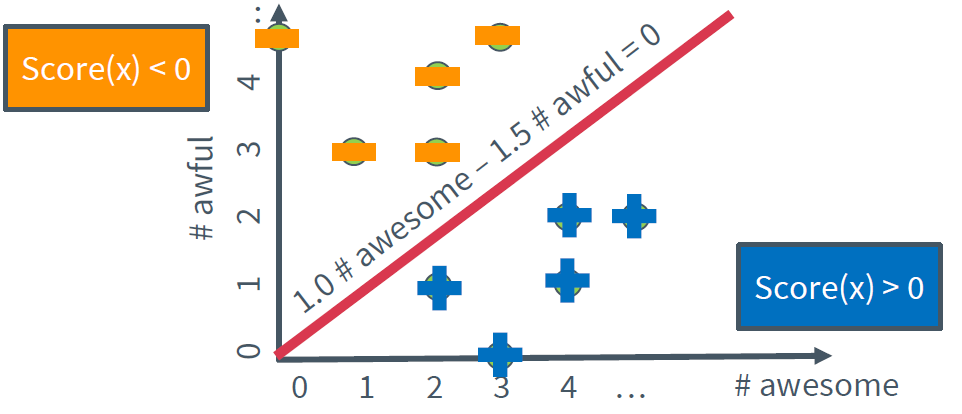
위와 같다. 따라서 빨간 선을 기준으로 위쪽은 score가 음수인 (부정적인) 리뷰글들, 아래쪽은 score가 양수인 (긍정적인) 리뷰글들이며 이러한 빨간 선을 decision boundary라 한다.
그런데 여기서 문제가 발생한다. 과연 우리는 이 linear classifier를 얼마나 신뢰할 수 있을까? 예를 들어 아래의 왼쪽과 같은 문장은 확실히 긍정적인 리뷰이지만 오른쪽 글은 긍정인지 부정인지 확신하기 어렵다.

여기서 확률의 개념이 사용된다. 예를 들어 y를 output label, x를 input sentence라 하면 아래와 같이 조건부 확률을 표현할 수 있다.

예를 들어 y=1이고 x가 입력된 리뷰글이면 해당 리뷰글이 긍정적일 확률이 된다. 만약 이 확률이 0.5보다 크면 긍정적, 0.5보다 작다면 부정적인 글이 될 것이며 결국 이 조건부 확률을 적절히 조절하는 것이 linear classifier을 학습시키는 최종 목표이다.
이제 score을 좀 더 일반적으로 표현해보자

w는 각 단어의 계수(weight), h는 각 단어의 계수를 의미한다. 결국 input sentence는 x와 w로 이루어지므로 확률은

로 표현된다. 문제는 이 확률이 score가 음의 무한대라면 0으로(긍정일 확률이 0), 양의 무한대라면 1로(긍정일 확률이 1) 0이라면 0.5가 돼야 할 것이다. 이 관계를 적절히 만족하는 함수가 바로 sigmoid 함수이다. sigmoid 함수는 다음과 같이 정의된다.
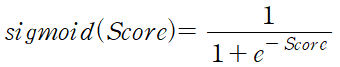

앞서 정의한 score function에 의해

가 된다.
이제 위 식을 이용하여 임의의 데이터셋에 대해 최적의 decision boundary를 계산해보자. 만약 최적의 decision boundary라면 각각의 조건부 확률이 가장 크게 표현돼야 하므로 (예를 들어 y=+1에서 긍정일 확률이 크고, y=-1에서 부정일 확률이 클수록 p(y|x, w)의 값은 커질 것이므로) 새로운 함수 l(w)를 다음과 같이 정의하자.

결국 이 l(w)를 최대로 만드는 w가 최적의 decision boundary를 결정할 것이다. 이제 maximize likelihood를 이용해 이 값의 최대값을 찾자. 계산의 편의를 위해 양변에 자연로그를 취한 함수를 ll(w)라 하면
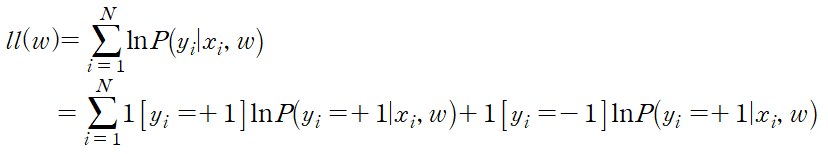
이다. 이때 1[y=+1]를 indicator function이라 하는데 y=1에서 1[y=+1]=1, y=-1에서 1[y=+1]=0을 만족하는 함수이다. (1[y=-1]은 반대) 따라서 아래 성질을 만족한다.

또한

이므로 정리하면

이다. gradient decent를 적용하기 위해 ll(w)의 gadient를 계산하면

이 된다.
우리는 maximize likelihood에 의해 이 값이 최대가 되길 원하므로 gradient decent가 아닌 gradient ascent가 된다. 위 식을 통해 구현한 gradient ascent 알고리즘은 아래와 같다.
 반응형
반응형'머신러닝 기초' 카테고리의 다른 글
Stochastic gradient descent (0) 2019.11.03 Logistic regression #2 (0) 2019.11.03 Geometric intuition of solution (0) 2019.10.12 Lasso Regression #3 (0) 2019.10.11 Lasso Regression #2 (0) 2019.10.09