-
Perceptron Algorithm머신러닝 기초 2019. 11. 10. 13:18반응형
Classification의 또 다른 알고리즘으로 perceptron 알고리즘이 있다. 예를 들어 y=-1과 y=+1의 2개의 class를 구분하는 linear classification을 생각해보자. 그러면 perceptron 알고리즘의 prediction은 다음과 같이 주어진다.

sign 함수는 아래와 같이 주어지는 함수이다.
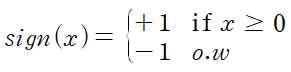
또한 weight의 초기값은 다음과 같다. (물론 random 한 값으로 초기화해도 무방하다.)

이제 perceptron 알고리즘은 아래와 같이 표현된다.
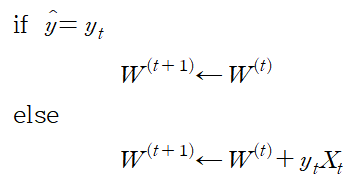
가중치를 업데이트하는 부분이 다소 이해가 안 될 수 있다. 하지만 예를 들어 y_t=+1이지만 y_hat, 즉 predict 값이 -1이라 가정하자. 따라서

값이 증가하여 양수가 돼야 하므로

를 만족한다 따라서 weight에 X_t를 더해 가중치를 업데이트해야 하므로

이고 1=y_t 이므로 주어진 식이 성립한다. y_t=-1인 경우도 동일하다.
perceptron 알고리즘은 모든 predict가 정확할 때까지 위 과정을 반복한다. predict가 실제 정답과 다른 경우를 mistake라고 하는데 perceptron은 이 mistake가 줄어드는 방향으로 학습한다. 아래와 같은 예를 들어보자.

만약 선형적으로 분리 가능한 데이터를 분리한다고 가정하자. 따라서

을 기준으로 두 데이터가 나뉜다. 이때 이 선과 데이터 사이의 거리를 의미하는 margin은 선을 기준으로 위쪽으로 양수, 아래쪽으로 음수이다. 이제 다음 조건을 만족한다고 하자.

여기서 감마는 데이터중 가장 가까운 margin을 의미하며 따라서 모든 데이터의 margin은 감마보다 크다. 이를 수식으로 표현하면

이다. 이제 아래 그림과 같이 모든 데이터들이 반지름이 R인 원 안에 분포한다 가정하면

mistake가 발생한 횟수 m에 대하여 다음 식을 만족한다.

이 부등식을 mistake bounds라고 하며 perceptron에서는 데이터 수와 관계없이 mistake의 수가 결정된다는 상당히 의미 있는 결론을 도출하게 된다. 이제 mistake bounds를 유도해보자. 우리는 앞서 설명한 weight의 업데이트 공식에서

를 만족한다.
또한 비슷하게

이다.
또 Cauchy-Schwartz 부등식에 의해

을 만족하므로 정리하면

을 만족하여 증명된다.
하지만 실제로 대부분의 경우 데이터가 선형적으로 분리되지는 않는다. 따라서 perceptron이 최적의 분류를 하는 기준이 필요하다.

위의 그래프에서도 알 수 있듯 최적의 weight는

으로 계산할 수 있다.
또한 gradient decent를 방식을 이용하기 위해 loss function이 필요한데, perceptron의 loss function은 아래와 같이 hinge loss(생긴 모양새 때문에 이름 붙여졌다.)로 표현된다.

수식으로 표현하면

이며 줄여서
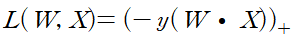
으로 표현된다.
따라서 perceptron이 최적의 분류를 하는 또 다른 기준은 이 hinge loss의 평균을 최소화하는 것이다.
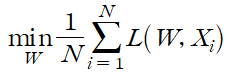
이제 gradient를 계산하기 위해 hinge loss를 미분해야 하는데, 문제는 hinge loss가 미분 불가능한 점이 존재하는 것이다. 따라서 subgradient를 이용해야 한다. 미분 값을 계산하여 한 줄로 표현하면 다음과 같다.
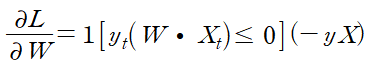
따라서 weight 업데이트 식은

SGD 형태로 표현하면
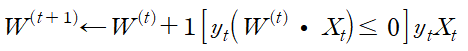
이 된다.
반응형'머신러닝 기초' 카테고리의 다른 글
Neural Networks #2 (0) 2019.11.25 Neural Networks #1 (0) 2019.11.15 Clustering (0) 2019.11.06 Nearest neighbor regression (0) 2019.11.03 Stochastic gradient descent (0) 2019.11.03