-
Clustering머신러닝 기초 2019. 11. 6. 17:43반응형
앞서 소개한 k-NN은 특정 데이터가 어느 데이터 군집에 제일 가까운지 계산하는 것이었다. 하지만 만약 여러 개의 데이터를 몇 개의 데이터 집합으로 분류하려면 어떻게 해야 할까?

예를 들어 뉴스 기사를 사회, 경제, 스포츠 등으로 분류하는 문제를 예를 들 수 있다. 이러한 학습은 정답이 정해져 있지 않기 때문에 unsupervised learning이라 불리며 이렇게 분류하는 방식을 clustering이라 한다.

위와 같이 뉴스 기사의 내용 중 특정 2개의 단어의 개수로 뉴스 기사를 표시하면 빨강, 초록, 파랑의 3개의 cluster(군집)으로 표현이 가능할 것이다. 따라서 clustering의 input은 데이터셋, output은 각 데이터 셋이 어느 cluster에 포함되는지에 대한 정보가 될 것이다.
그렇다면 cluster는 어떻게 정의될까? 아래 그림과 같이 임의의 데이터 x_i의 cluster는 각 cluster들의 중심까지의 거리가 가장 짧은 cluster로 정의된다.

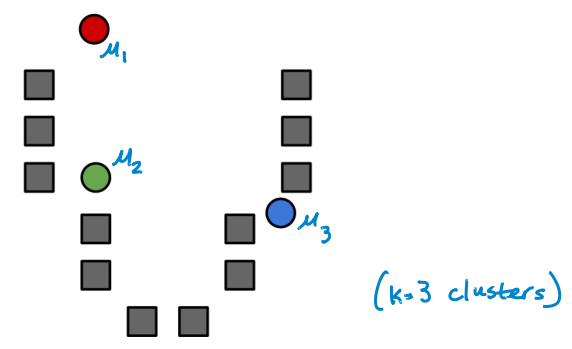
물론 데이터들의 분포에 따라 clustering이 쉬울 수도 어려울 수도 있다. 이제 본격적으로 clustering algorithm에 대해 알아보자. 대표적인 clustering algorithm으로 k-means가 있다. 우선 아래와 같은 데이터 포인트들이 있다고 가정하자.

이제 cluster centers(cluster 중심)을 초기화한다. 만약 3개의 cluster가 필요하다면 다음과 같이 임의의 위치에 3개의 cluster centers를 설정하면 된다. 각각의 cluster center를 u_1, u_2, u_3라 하자.
이제 각각의 데이터를 가장 가까운 cluster center에 따라 cluster를 할당한다. 이를 수식으로 표현하면 다음과 같다.
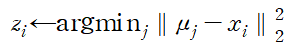
i 번째 데이터와 j번째 cluster center의 거리를 측정하여 가장 짧은 거리의 cluster를 반환한다. 이를 시각화하면 다음과 같다.

각 색깔 영역은 특정 cluster center과 가장 가까운 영역이다. 예를 들어 초록색 영역의 모든 데이터셋은 초록색 cluster center와 가장 가깝다.
이제 이렇게 분류된 데이터들을 이용해 cluster center를 수정한다. 수정된 cluster center는 다음과 같이 표현된다.
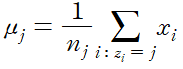
n_j는 j번째 포함된 데이터의 총 개수로 따라서 수정된 cluster center는 각 cluster에 포함된 데이터들의 무게중심이라 봐도 무방하다. 실제로 이 지점은

를 최소화하는 지점이다. 이를 증명해보자.
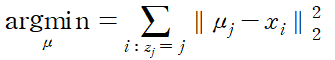
위 식을 편미분 하면

이므로 성립한다.
이제 이 cluster center를 이용해 위의 과정을 계속 반복하면 결국 각 cluster center는 특정한 위치로 수렴하게 된다.

k-means 알고리즘은 이러한 점에서 coordinate decent 알고리즘과 상당히 유사하다. 사실 k-means 알고리즘은 global optimum이 아닌 local optimum으로 수렴한다는 특징이 있다. 따라서 초기 cluster center의 위치가 매우 중요한데 아래 그래프와 같이 초기 cluster center의 위치(십자가)에 따라 결과는 매우 달라진다.
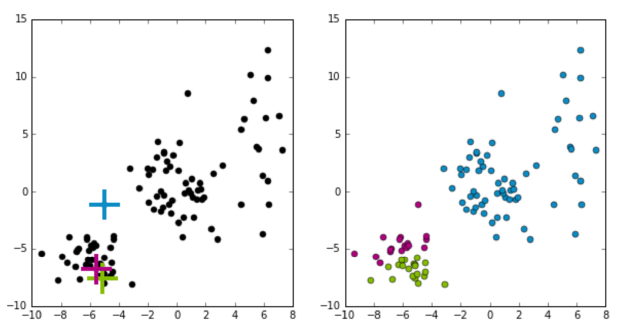
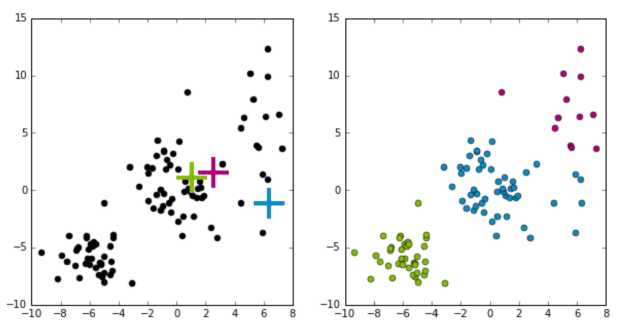
그렇다면 어떤 k-means의 결과가 더 좋다고 말할 수 있을까? 일반적으로 k-means 알고리즘은 데이터와 cluster center 사이의 제곱 거리를 최소화한다. 따라서 두 그래프의 아래 식의 값을 비교하면 더 좋은 k-means 결과를 결정할 수 있다.
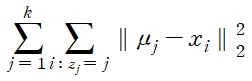
이 값은 흔히 heterogeneity라 불리며 값이 작을수록 더 좋은 k-means의 결과를 의미한다. 그렇다면 k는 어떤 값으로 설정해야 할까. 극한의 상황을 가정하여 k=N이라 할 수 있겠다. 이 경우 cluster의 개수가 데이터수와 같기 때문에 k-means의 결과 heterogeneity는 0으로 수렴할 것이다. 하지만 분명히 이것이 좋은 결과는 아니다. 실제로 k의 크기에 따라 heterogeneity의 크기를 비교하면 아래 그래프와 같다.
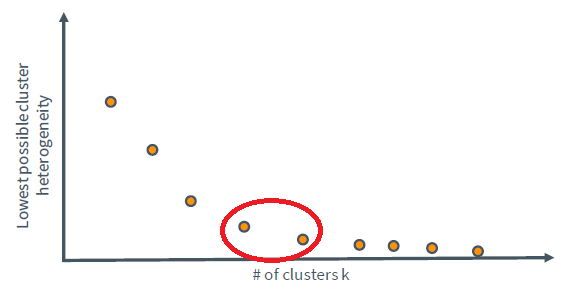
일반적으로 빨간색으로 표시된 지점의 k가 적절한 k라고 알려져 있다. (그래프가 꺾이는 부분) 물론 이것은 추측일 뿐이며 상황에 따라 바뀔 수 있다.
반응형'머신러닝 기초' 카테고리의 다른 글
Neural Networks #1 (0) 2019.11.15 Perceptron Algorithm (0) 2019.11.10 Nearest neighbor regression (0) 2019.11.03 Stochastic gradient descent (0) 2019.11.03 Logistic regression #2 (0) 2019.11.03