Neural Networks #3

실제로 neural network를 이용해 학습을 하는 과정은 매우 어려운 과정이다. 특히 아래와 같은 gradient descent 식에서

 

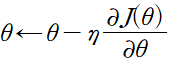
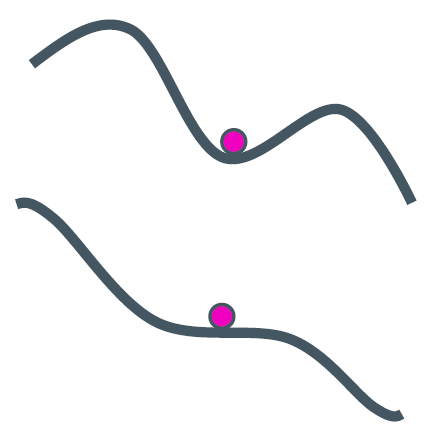
learning rate를 결정하는 것은 매우 어렵다. learning rate가 너무 작다면 학습 속도가 느리며 local minima에 갇힐 수 있다. 반대로 learning rate가 너무 크다면 학습이 불안정해지고 발산할 수 있다. 실제로 매 학습마다 적절한 learning rate를 새로 결정하는 것은 매우 어렵기 때문에 adaptive learning rate라는 방식을 사용한다. 대표적으로 momentum, adagrad, adadelte, RMSProp, adam 등이 존재한다. 이러한 알고리즘은 아래 그림과 같이 SGD 등이 local minima나 saddle point에 같이는 현상을 막는다.

 

예를 들어 momentum은 SGD와 비교했을 때 momentum과 관련된 항이 추가된다.

 

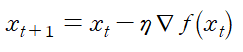
SGD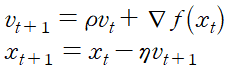

SGD+Momentum

벡터 그림으로 표현하면 아래와 같다.

 

위 식을 다시 적으면

 

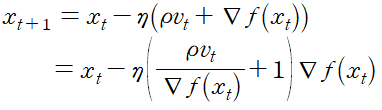
로 새로운 learning rate가 결정된다.

 

실제로 각각의 optimization algorithm들을 비교해보면 아래와 같다.

 

 

 

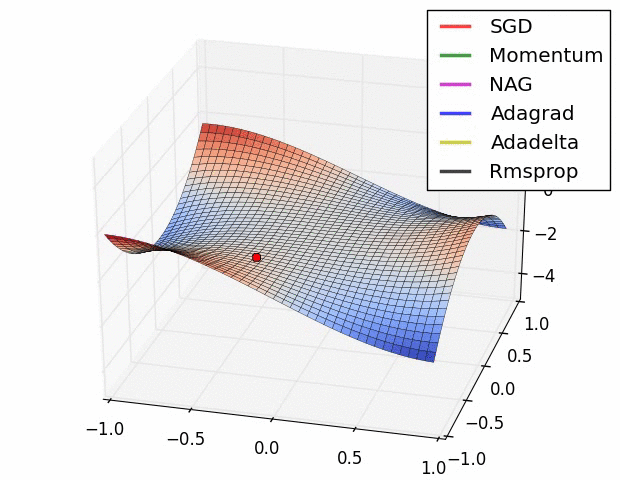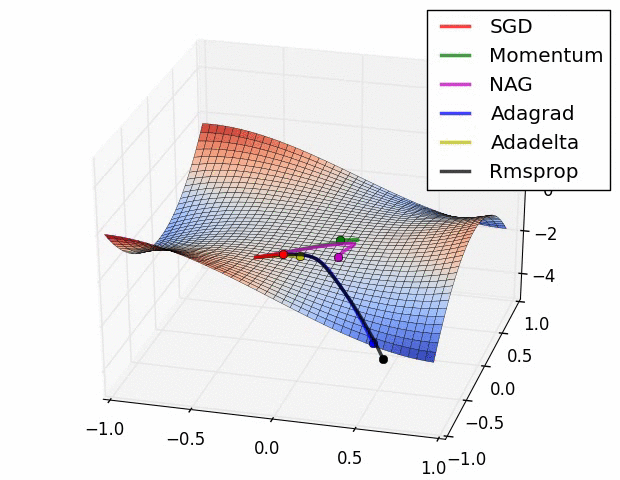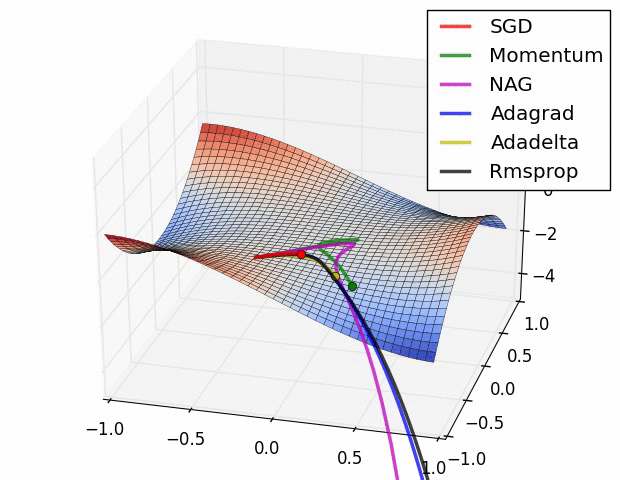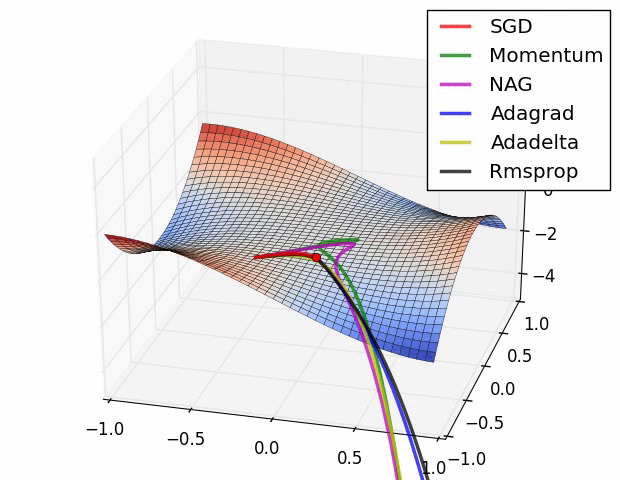
위와 같이 모든 경우에서 SGD는 다른 알고리즘들에 비해 성능이 월등하게 낮다. 다른 알고리즘들 보다 이동속도가 현저하게 느릴 뿐만 아니라, 방향을 제대로 잡지 못하고 이상한 곳에서 수렴하여 이동하지 못하는 모습도 관찰할 수 있다. 즉 단순한 SGD를 이용하여 네트워크를 학습시킬 경우 네트워크가 상대적으로 좋은 결과를 얻지 못할 것이라고 예측할 수 있다.

 

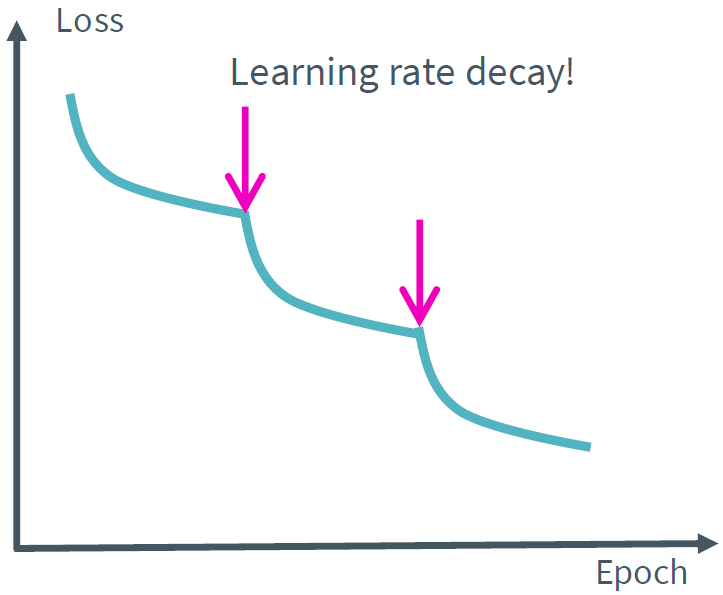
또 다른 방법은 학습이 진행됨에 따라 lenrning rate를 감소시키는 것이다. 각 learning rate에 따른 loss의 변화는 아래와 같다.

 

 

learning rate가 크면 loss가 감소하지 못하고 특정값에 수렴함을 확인할 수 있다. 이 경우 특정 두 지점을 진동하고 있음을 의심해볼 수 있는데 이때 learning rate를 감소시키면 아래와 같이 정상적으로 학습이 될 수 있다.

 

 

학습의 효율을 높이는 방법으로는 mini-batch를 사용하는 방법도 존재한다. 아래는 일반적인 GD, SGD mini-batch SGD의 알고리즘 차이를 보여준다.

 

gradient descent

stochastic gradient descent

mini-batch stochastic gradient descent

 

mini-batch는 SGD의 불안정한 학습을 막고 gradient descent의 느린 학습 속도를 보완하여 빠른 학습 속도를 보여준다.

 

activation function은 각 함수마다 장단점을 가지고 있다. 초기에는 실제 신경에서의 뉴런 반응과 비슷한 sigmoid 함수가 많이 사용되었다.

 

 

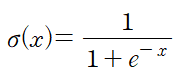
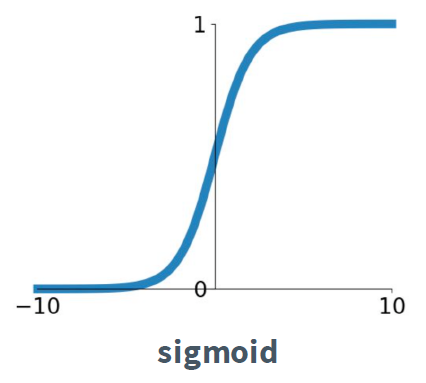
문제는 입력값이 크거나 작으면 (예를 들어 10, -10) 아래와 같이 gradient가 0이 된다는 것이다.

 

 

 

이를 vanishing gradient problem이라 부른다. gradient는 미분값 즉 변화량을 의미하는데, 이 변화량이 매우 작다면, network를 효과적으로 학습시키지 못하고 수렴해버리는 문제가 발생한다는 것이다. 즉 input에서는 큰 변화가 있다고 하더라도, output에는 작은 변화를 보이게 된다.  gradient가 작기 때문이다.

두 번째로 sigmoid가 not zero-centered란 문제가 존재한다. 2개의 sigmoid output을 x_1, x_2라 하고

 

라고 하자. x_1, x_2는 항상 양수이므로

 

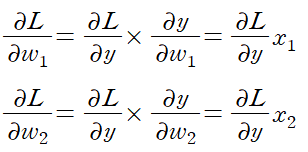
가 모두 같은 부호를 가진다. 따라서 weight가 모두 양수, 또는 모두 음수인 방향으로만 업데이트된다. 이를 그래프로 나타내면 아래와 같이 지그재그 모양으로 보인다.

 

 

마지막으로 exp() 함수는 계산에 필요한 비용이 크다는 문제도 존재한다.

 

비슷하게 tanh(x) 함수도 있다.

 

이 activation function은 zero-centered 하지만 vanishing gradient problem이 여전히 존재한다.

 

실제로 가장 많이 사용되는 activation function은 ReLU이다.