Neural Ordinary Differential Equations (Neural ODE) [작성 중]

https://arxiv.org/abs/1806.07366

Neural Ordinary Differential Equations

 

Neural Ordinary Differential Equations (이하 Neural ODE)는 2018년도 NeurIPS에서 best paper award를 받은 논문이다. 수식적으로 이해하기 상당히 어렵지만 이해해두면 좋을 것 같아 틈틈이 정리해볼까 한다.

 

먼저 ResNet으로 유명한 residual block의 구조를 다시 한번 봐보자. ResNet는 전에 정리해둔 글이 있다.

https://hydragon-cv.info/entry/Deep-Residual-Learning-for-Image-Recognition

Deep Residual Learning for Image Recognition

 

위 그림을 논문 수식 형태로 다시 표현하면 아래와 같다.

 

$h _ { t+1 } =h _ { t } + F \left ( h _ { t } , \theta _ { t } \right )$

 

따라서 $h _ { t+1 } -h _ { t } =F \left ( h _ { t } , \theta _ { t } \right )$인데, t의 변화량이 매우 작다면 다음과 같이 표현할 수 있을 것이다.

 

$\frac{ dh \left ( t \right ) } { dt } =f \left ( h \left ( t \right ) ,t, \theta \right )$

 

뉴럴 네트워크에서 $t$의 변화량이 매우 작다는 것은 일반적이지 않지만 위와 같은 레이어가 네트워크에 무수히 많이 쌓여있다고 생각하면 고려할 수 있다. 다시 말해 일반적엔 네트워크가 layer를 통과하면서 값이 이산적으로 변화하겠지만 이를 연속적인 변화로 간주할 수 있다는 것이다.

 

 

저자들은 위 식이 상미분 방정식 (ordinary differential equations, 독립 변수를 하나만 포함하며, 하나 이상의 도함수를 가지고 있는 미분방정식)와 형태가 유사하다는 것에 주목하는데, 실제로 상미분 방정식의 일반 형태는 $\frac{ dz } { dt } =f \left ( z,t \right )$로 매우 유사하다.

 

결과적으로 이산적이지 않은, 연속적인 뉴럴 네트워크의 임의의 지점에서의 값을 계산하기 위해서는 위 상미분 방정식의 해를 구하는 것과 동일한다. 아래 그림을 보면 이해가 편하다.

 

 

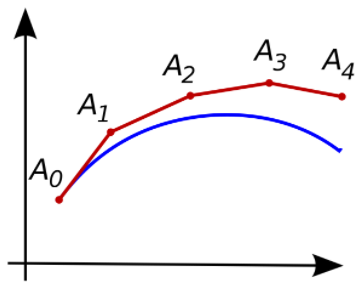
위 그래프의 파란색 곡선이 실제 연속적인 레이어를 통과하면서 변화하는 값이라고 가정하자. 일반적인 함수의 경우 초기값 $A _{0}$를 알고 있다면 상미분 방정식의 해는 유일함이 알려져 있는데, 위 상미분 방정식을 풀 수만 있다면 파란색 곡선을 도출하는 것이 가능하다. 이를 근사하는 유명한 방법 중 하나가 바로 오일러 (Euler) 방법이다. 오일러 방법은 아래와 같다.

 

$y _{i+1} =y _{i} +f \left( t _{i} ,y _{i} \right) h$

 

위와 같은 방법으로 $t_i$에서의 함수 값을 알면 위 과정을 반복하여 그래프를 근사하는 것이 가능하다. (이 전 그래프의 $A_0$, $A_1$, $A_2$, $A_3$, $A_4$와 유사하며, 단점은 오일러 방법은 뒤로 갈수록 오차가 누적된다는 점이다.) 오일러 방법을 반복해서 그래프를 근사하는 자세한 방법은 아래 글을 참고하면 된다.

https://angeloyeo.github.io/2021/04/30/direction_fields.html

방향장과 오일러 방법 - 공돌이의 수학정리노트

 

어쨌든 이러한 방식을 사용하면 네트워크의 출력 값들을 근사할 수는 있겠지만 이러한 방식은 큰 메모리 비용이 발생하여 비효율적이다. 따라서 저자들은 이러한 상미분 방정식의 해를 효과적으로 계산할 수 있는 adjoint sensitivity method를 이용한다.

 

먼저 지금까지의 과정을 수식으로 정리하면 아래와 같다. (논문에서 $h$가 $z$로 바뀌었다.)

 

 $z \left ( t _ { 1 } \right ) =z \left ( t _ { 0 } \right ) + \int _ { t _ { 0 } } ^ { t _ { 1 } } { \frac{ dz \left ( t \right ) } { dt } dt } =z \left ( t _ { 0 } \right ) + \int _ { t _ { 0 } } ^ { t _ { 1 } } { f \left ( z \left ( t \right ) ,t, \theta _ { t } \right ) dt }$

 

그래프를 그려보면 당연한 수식이다. 이 값을 참값과 비교해야 하기 때문에 이를 loss function $L$에 집어 넣으면

 

$L \left ( z \left ( t _ { 1 } \right ) \right ) =L \left ( z \left ( t _ { 0 } \right ) + \int _ { t _ { 0 } } ^ { t _ { 1 } } { f \left ( z \left ( t \right ) ,t, \theta _ { t } \right ) dt } \right )$

 

와 같다. 네트워크를 학습하기 위해서는 위 loss function의 에러 값을 최소화하는 방향으로, 즉 $L \left ( z \left ( t _ { 1 } \right ) \right )$를 최소화 하는 방향으로 학습한다.

 

일반적인 역전파 연산은 parameter에 대한 gradient $\frac{ \partial L } { \partial \theta }$를 계산하는 것임을 알고 있을 것이다. 결국에 우리가 계산하고 싶은 것은 주어진 loss function $L$과 model parameter $\theta$ 에 대해서 gradient $\frac{ \partial L } { \partial \theta }$를 계산하고 싶은 것인데, adjoint sensitivity method는 이를 계산하기 위해서 adjoint $a \left ( t \right ) = \frac{ \partial L } { \partial z \left ( t \right ) }$를 정의하게 된다.