-
Up-sampling with Transposed Convolution [번역]머신러닝, 딥러닝 공부 2020. 2. 18. 19:48반응형
원문 : https://medium.com/activating-robotic-minds/up-sampling-with-transposed-convolution-9ae4f2df52d0
Up-sampling with Transposed Convolution
If you’ve heard about the transposed convolution and got confused what it actually means, this article is written for you.
medium.com
만약 여러분이 transposed convolution에 대해 듣고 그것이 실제로 무엇을 의미하는지 혼란스러워했다면, 이 글은 여러분을 위해 쓰인 것이다.
이 글의 내용은 다음과 같다:
- The Need for Up-sampling
- Why Transposed Convolution?
- Convolution Operation
- Going Backward
- Convolution Matrix
- Transposed Convolution Matrix
- Summary
The Need for Up-sampling
우리가 neural network를 사용하여 이미지를 생성할 때, 그것은 보통 낮은 해상도에서 높은 해상도로 up-sampling을 수반한다.
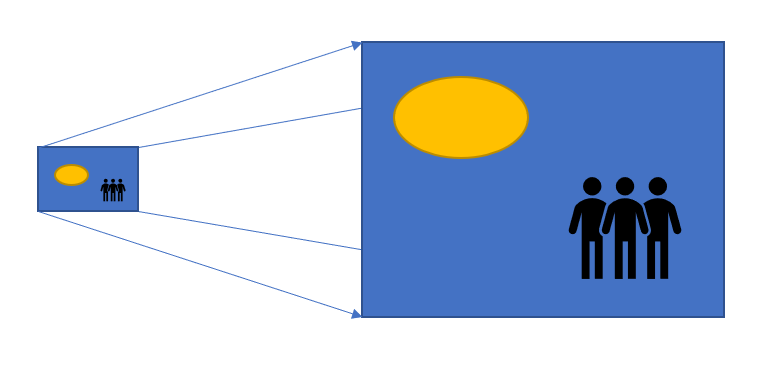
up-sampling 작동을 수행하는 방법은 다양하다 :
- Nearest neighbor interpolation
- Bi-linear interpolation
- Bi-cubic interpolation
이 모든 방법들은 우리가 network architecture를 결정할 때 선택할 필요가 있는 몇 가지 interpolation(보간법)을 포함한다. 그것은 manual feature engineering과 같으며 network가 배울 수 있는 것은 아무것도 없다.
Why Transposed Convolution?
만약 우리가 우리의 network가 최적의 up-sample 방법을 배우길 원한다면, 우리는 transposed convolution을 사용할 수 있다. 사전 정의된 interpolation을 사용하지 않는다. 그것은 학습할 수 있는 parameter를 가지고 있다.
다음과 같은 중요한 논문과 프로젝트에서 사용되므로, transposed convolution 개념을 이해하는 것이 유용하다 :
- the generator in DCGAN takes randomly sampled values to produce a full-size image.
- the semantic segmentation uses convolutional layers to extract features in the encoder and then restores the original image size in the decoder so that it can classify every pixel in the original image.
참고로 transposed convolution은 다음과 같이 알려져 있다:
- Fractionally-strided convolution
- Deconvolution
우리는 이 글에서 transposed convolution이라는 단어만 사용할 것이지만 다른 글에서는 다른 명칭으로 사용될 수 있다.
Convolution Operation
간단한 예를 들어 convolution 계산이 어떻게 작동하는지 설명해보자. 4x4 매트릭스를 가지고 있으며 3x3 kernel에 padding이 없고 1의 stride로 convolution 연산을 적용한다고 가정해 보자. 아래에 보이는 바와 같이 출력은 2x2 매트릭스다.
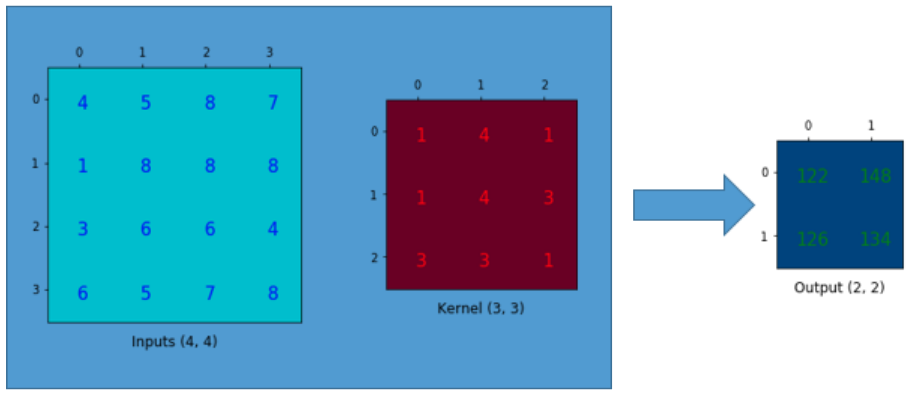
convolution 연산에서는 입력 매트릭스와 커널 매트릭스 사이의 원소 곱셈 합계를 계산한다. padding도 없고 1의 stride도 없기 때문에 이것을 단지 4번만 수행할 수 있다. 따라서 출력 매트릭스는 2x2이다.
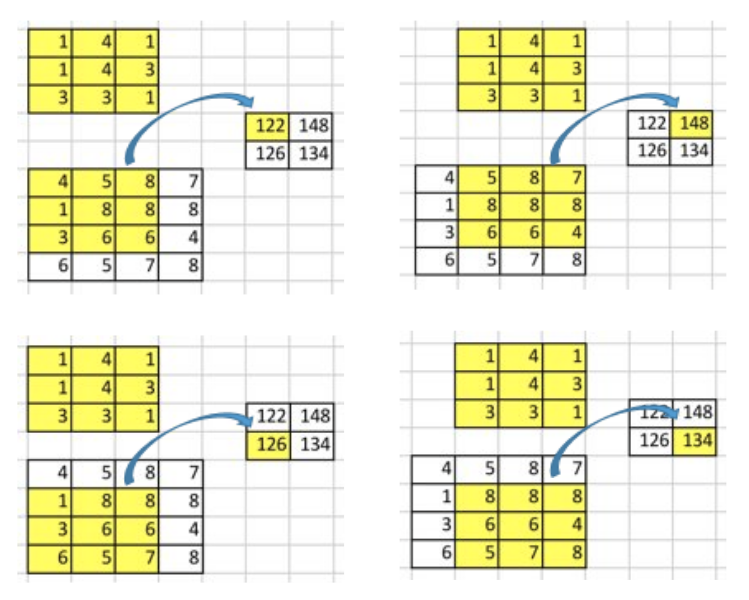
그러한 convolution의 중요한 포인트 중 하나는 입력 값과 출력 값 사이에 위치 연결이 존재한다는 것이다.
예를 들어 입력 매트릭스의 왼쪽 상단 값은 출력 매트릭스의 왼쪽 상단 값에 영향을 미친다.
보다 구체적으로는 3x3 kernel을 사용하여 입력 매트릭스의 9 값을 출력 매트릭스의 1 값에 연결한다. convolution 연산은 다대일(many-to-one) 관계를 형성한다. 이를 명심하고 있자.
Going Backward
이제, 우리가 다른 방향으로 가고 싶다고 가정하자. 우리는 행렬의 1 값을 다른 행렬의 9 값에 연결하기를 원한다. 일대다(one-to-many) 관계다. 이것은 마치 convolution 연산을 거슬러 올라가는 것과 같으며, 그것은 transposed convolution 연산의 핵심 개념이다.
예를 들어, 우리는 2x2 행렬을 4x4 행렬로 up-sample 한다. 연산은 1-to-9 관계를 유지한다.
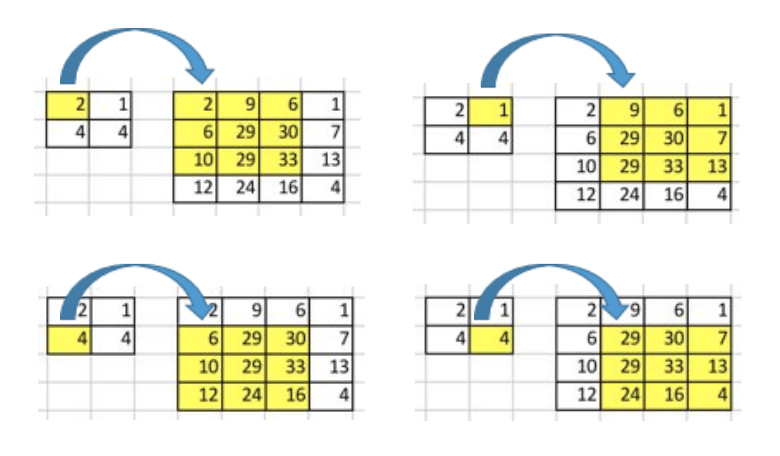
그러나 우리는 어떻게 그런 연산을 수행할 것인가?
그 방법에 대해 이야기하려면, 우리는 convolution 매트릭스와 transposed convolution 매트릭스를 정의해야 한다.
Convolution Matrix
우리는 매트릭스를 이용하여 convolution 연산을 표현할 수 있다. 그것은 우리가 매트릭스 곱셈을 사용하여 convolution 연산을 수행할 수 있도록 재배열된 kernel 매트릭스에 불과하다.

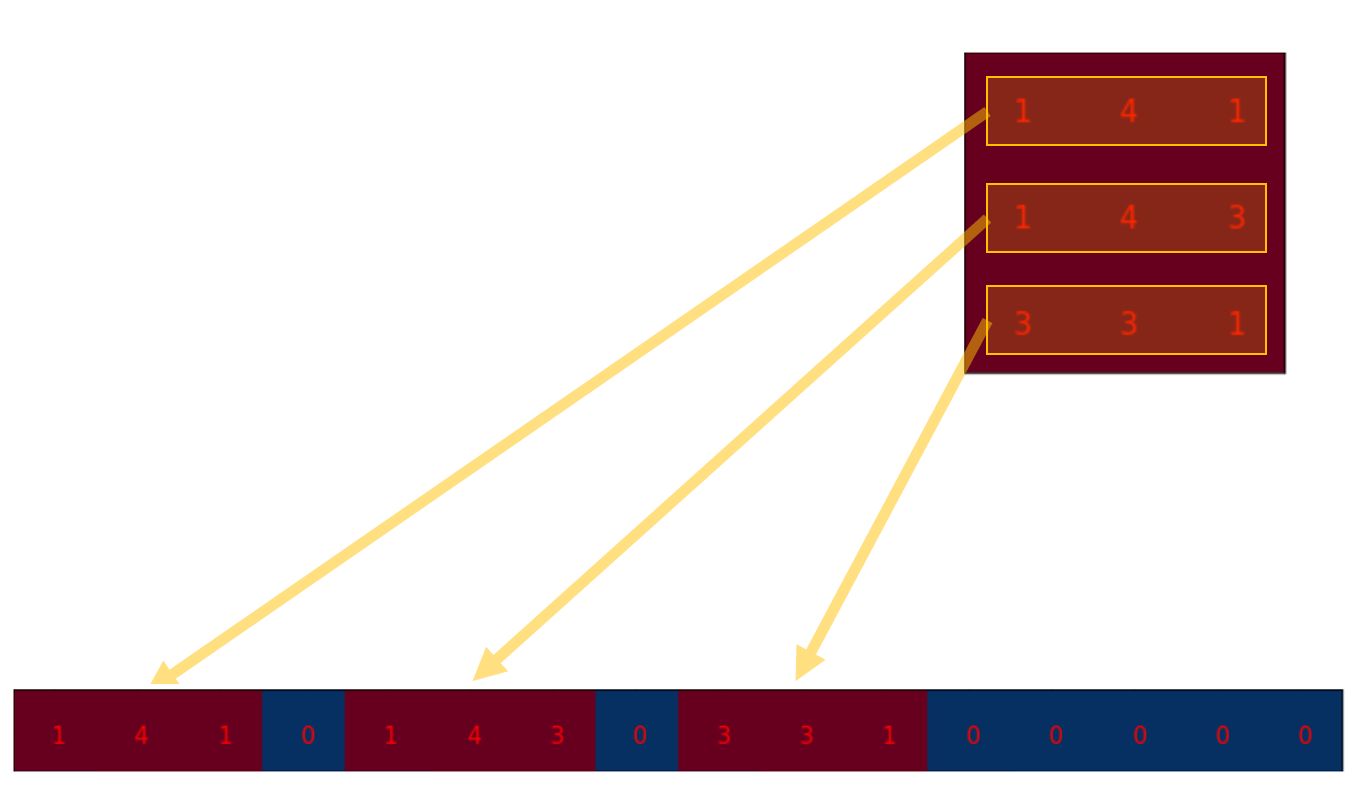
3x3 커널을 아래와 같이 4x16 매트릭스로 재배열한다 :

이게 바로 convolution 매트릭스다. 각 행은 하나의 convolution 연산을 정의한다. 만약 잘 이해가 안 된다면, 아래의 도표가 도움이 될 것이다. convolution 매트릭스의 각 행은 서로 다른 장소에 padding이 0인 재조정된 커널 매트릭스에 불과하다.
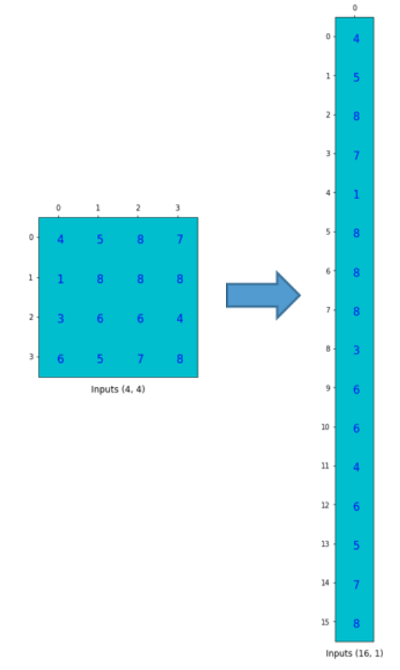
그것을 사용하기 위해 입력 매트릭스(4x4)를 열 벡터(16x1)로 평탄(flatten)하게 한다.
16x1 입력 매트릭스(16차원 열 벡터)를 사용하여 4x16 convolution 매트릭스를 곱할 수 있다.
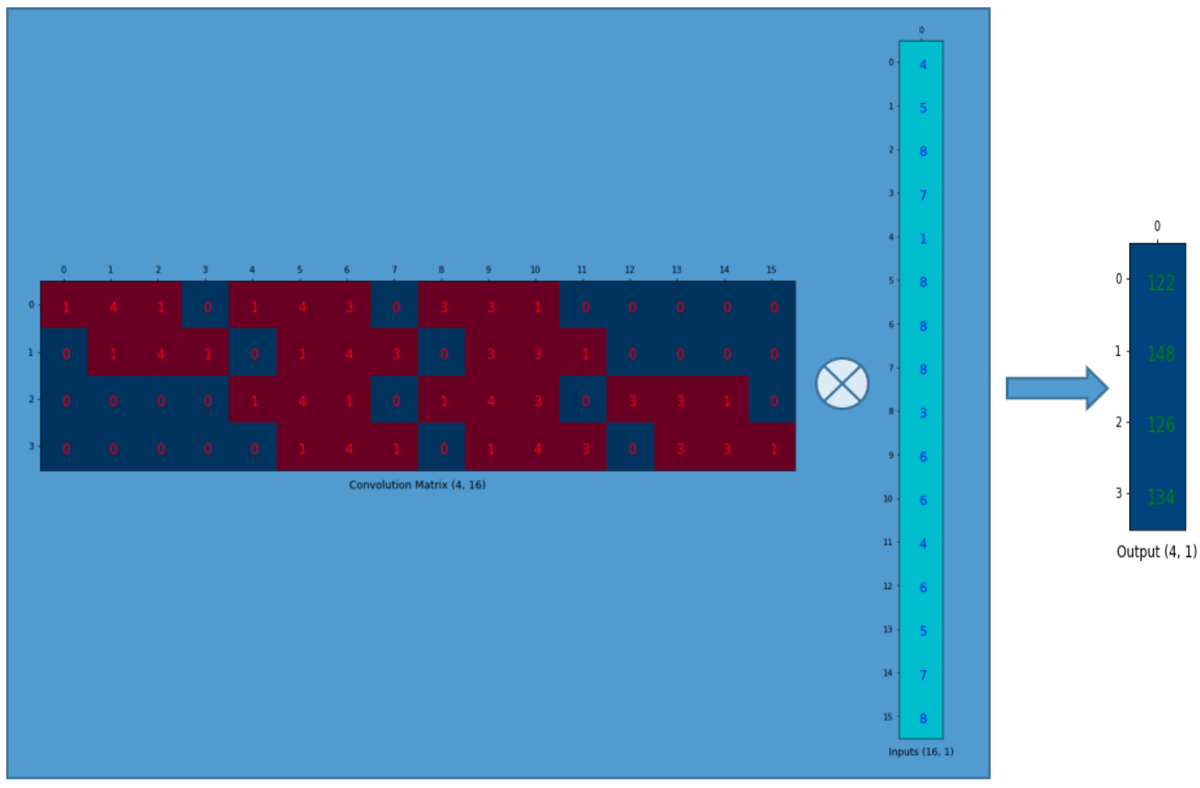
출력 4x1 매트릭스는 이전과 동일한 결과를 제공하는 2x2 매트릭스로 재구성될 수 있다.

간단히 말해서, convolution matrix는 재배열된 kernel weight에 지나지 않으며, convolution 연산은 convolution matrix를 사용하여 표현할 수 있다.
요점은 convolution 매트릭스가 4x16이기 때문에 convolution 매트릭스를 사용하면 16(4x4)에서 4(2x2)로 갈 수 있다는 것이다. 그러면 16x4 매트릭스가 있으면 4(2x2)에서 16(4x4)으로 갈 수 있다.
Transposed Convolution Matrix
우리는 4(2x2)에서 16(4x4)로 가고 싶다. 그래서 우리는 16x4 매트릭스를 사용한다. 하지만 여기에 한 가지 더 있다. 우리는 1에서 9까지의 관계를 유지하고 싶다.
convolution 매트릭스 C(4x16)를 C.T(16x4)로 변환한다고 가정해 보자. 열 벡터(4x1)와 C.T(16x4)를 곱하여 출력 매트릭스(16x1)를 생성할 수 있다. 전치된 매트릭스는 출력에서 1 값을 9 값으로 연결한다.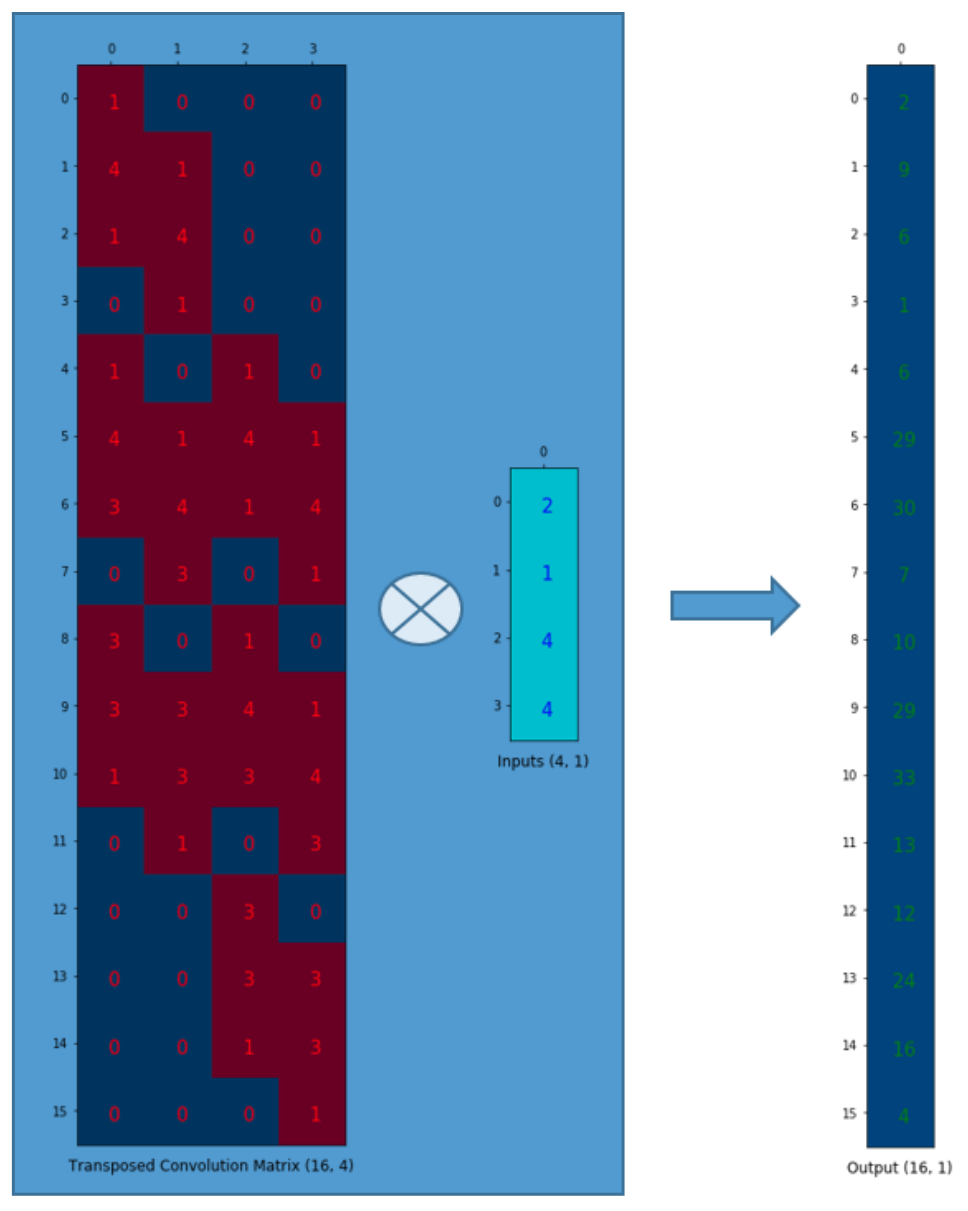
출력은 4x4로 재형성할 수 있다.

우리는 방금 더 작은 매트릭스(2x2)를 더 큰 매트릭스(4x4)로 up-sample 했다. transposed convolution은 weight를 배치하는 방식 때문에 1에서 9까지의 관계를 유지한다.
NB: 행렬의 실제 weight 값은 원래 convolution 매트릭스에서 올 필요가 없다. 중요한 것은 weight 배열이 convolution 매트릭스로부터 전이(transposed)된다는 것이다.
Summary
transposed convolution 연산은 일반적인 convolution과 동일한 연결을 형성하지만 backward 방향으로 이루어진다.
우리는 그것을 이용해서 up-sampling을 만들 수 있다. 게다가, transposed convolution의 weight는 학습할 수 있다. 그래서 우리는 사전 정의된 보간법이 필요하지 않다.
비록 그것이 transposed convolution이라고 불리지만, 그것은 우리가 기존의 어떤 convolution 매트릭스를 취해서 transposed 된 버전을 사용한다는 것을 의미하지는 않는다. 입력과 출력의 연관성은 표준 convolution 매트릭스(일대다 연결보다는 다대일 연결)와 비교했을 때 backward으로 처리된다는 것이 요점이다.
이와 같이 transposed convolution은 convolution이 아니다. 하지만 우리는 convolution을 사용해서 transposed convolution을 모방할 수 있다. 우리는 입력 매트릭스의 값 사이에 0을 추가하여 transposed convolution과 동일한 효과를 내는 방식으로 입력을 up-sample 한다. 당신은 어떤 글이 이러한 방식으로 transposed convolution을 설명하는 것을 발견할 수 있을 것이다. 단, convolution 전에 입력을 up-sample 하기 위해 0을 추가해야 하기 때문에 효율성이 떨어진다.
한 가지 주의할 점은, transposed convolution가 생성된 영상에서 checkerboard artifacts의 원인이라는 것이다. 이 글은 이러한 문제를 줄이기 위해 up-sampling 연산(즉, 보간법)을 권장한다. 만약 당신의 주된 목적이 그러한 과정 없이 이미지를 생성하는 것이라면, 더 많은 것을 알아내기 위해 논문을 읽을 가치가 있다.References
[1] A guide to convolution arithmetic for deep learning
Vincent Dumoulin, Francesco Visin
https://arxiv.org/abs/1603.07285
[2] Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks
Alec Radford, Luke Metz, Soumith Chintala
https://arxiv.org/pdf/1511.06434v2.pdf
[3] Fully Convolutional Networks for Semantic Segmentation
Jonathan Long, Evan Shelhamer, Trevor Darrell
https://people.eecs.berkeley.edu/~jonlong/long_shelhamer_fcn.pdf
[4] Deconvolution and Checkerboard Artifacts
Augustus Odena, Vincent Dumoulin, Chris Olah
반응형'머신러닝, 딥러닝 공부' 카테고리의 다른 글
Fully Convolutional Networks for Semantic Segmentation (0) 2020.03.01 An Introduction to different Types of Convolutions in Deep Learning [번역] (0) 2020.02.27 Accelerating the Super-Resolution Convolutional Neural Network (0) 2020.02.16 Spatial Transformer Networks (0) 2020.02.08 Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization (0) 2020.02.07